How many geometric progressions are possible containing 27, 8 and 12 as three of its/their terms
A
One
B
Two
C
Four
D
Infinitely many
Video Solution
Text Solution
The correct Answer is:D
Let 'a' be the first term & 'x' be the common ratio. Also, suppose 27, 8 & 12 be the pth,qth & rth term of the GP.
∴ axp−1=27
axq−1=8
&axr−1=12
Now, 27×82=123
⇒axp−1x(axq−1)2=(axr−1)3
⇒xp−1.x2q−2=x2r−3
⇒p−1+2q−2=3r−3
⇒p+2q−3r=0 ...(1)
There are infinitely many solutions for the eq. (1).
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
How many geometric progressios is/are possible containing 27.8 and 12 as three of its/their terms ?
AOneBTwoCFourDInfinitely many - Question 2 - Select One
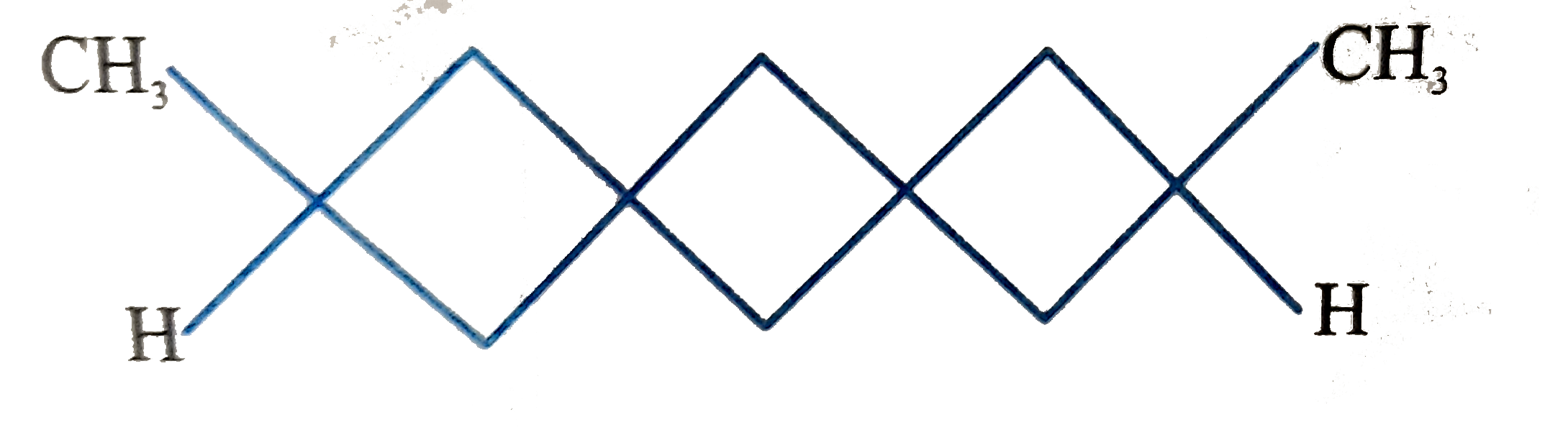
How many geometrical isomers are possible for
 A2B3C4D8
A2B3C4D8 - Question 3 - Select One
How many geometrical isomers of this compound are possible ?
 A0B2C3D4
A0B2C3D4
Does there exist a geometric progression containing 27,8 and 12 as three of its term ? If it exists, then how many such progressions are possible ?
View Solution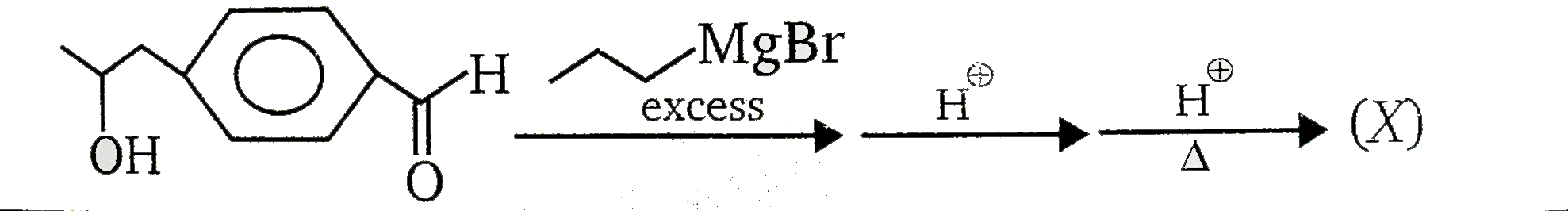
How many geometrical isomer of (X) is possible ?View Solution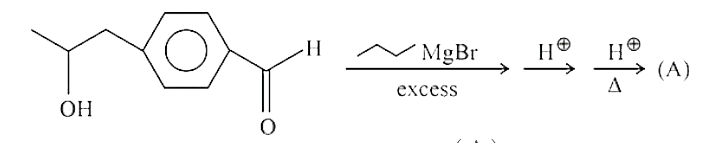
How many geometrical isomer of (A) is possible?View SolutionThere are infinite geometric progressions of for which 27,8 and 12 are three of its terms (not necessarily consecutive). Statement 2: Given terms are integers.
View SolutionHow many geometrical isomers are possible for following compound
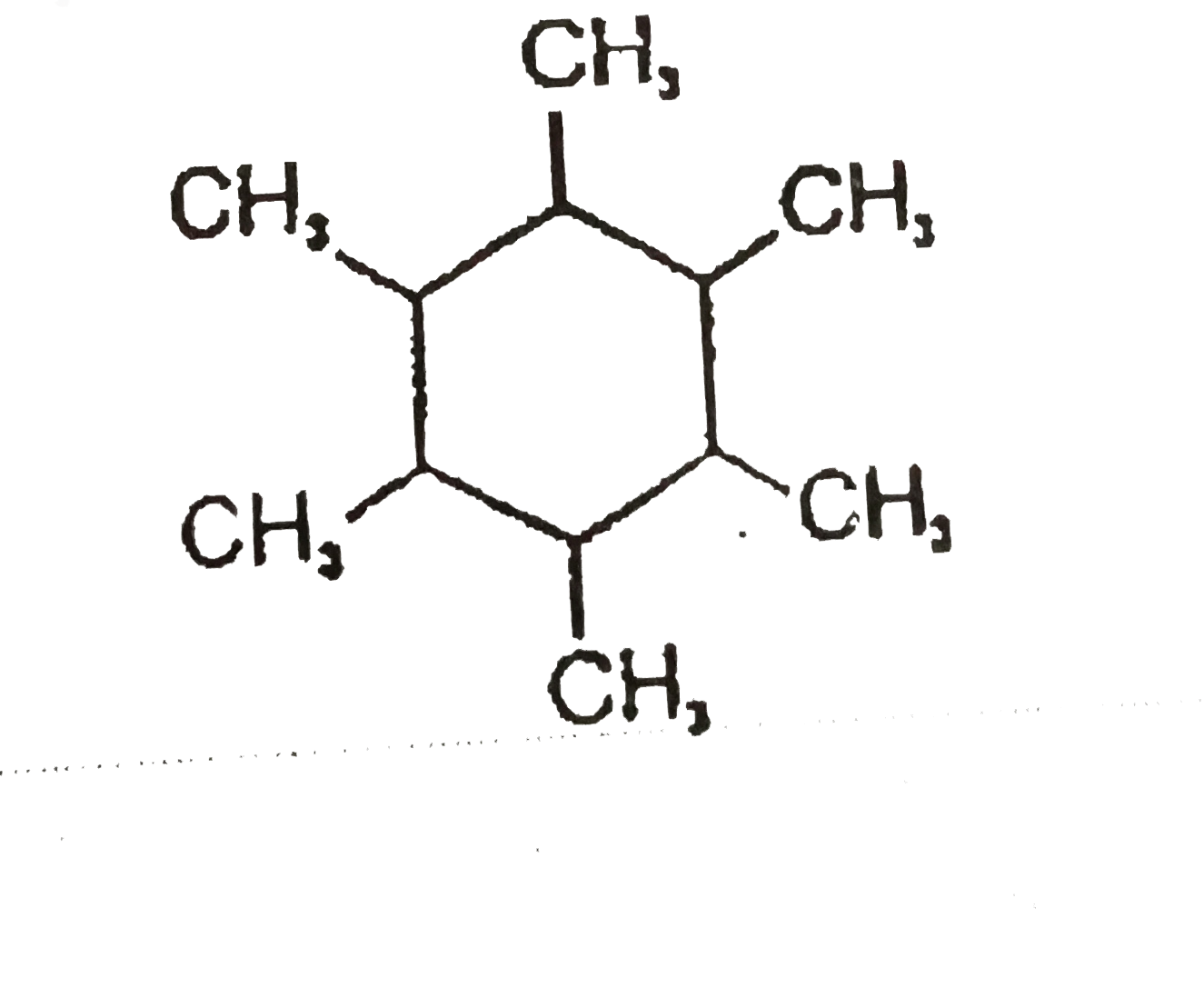 View Solution
View Solution