Under what condition does A (BC) = (AB)C hold, where A, B, C are three matrices ?

A

AB and BC both must exist

B

Only Ab must exist

C

Only BC must exist

D

Always true

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To determine the condition under which the equation $A (B C) = (A B) C$ holds for three matrices $A$ , $B$ , and $C$ , we need to explore the properties of matrix multiplication, specifically the associative property.
1. Understanding Matrix Multiplication:
- Matrix multiplication is not commutative, meaning $A B \neq B A$ in general. However, it is associative, which means that the way in which matrices are grouped during multiplication does not change the result, provided the matrices are compatible for multiplication.
2. Identifying Compatibility:
- For the expression $A (B C)$ to be valid, the matrices $B$ and $C$ must be compatible for multiplication. This means that the number of columns in $B$ must equal the number of rows in $C$ .
- For the expression $(A B) C$ to be valid, the matrices $A$ and $B$ must also be compatible for multiplication, which means the number of columns in $A$ must equal the number of rows in $B$ .
3. Conditions for Equality:
- The equation $A (B C) = (A B) C$ holds true if both products $A B$ and $B C$ are defined. Therefore, we need to ensure that:
- $A$ has the same number of columns as $B$ has rows.
- $B$ has the same number of columns as $C$ has rows.
4. Conclusion:
- The condition under which $A (B C) = (A B) C$ holds is that both products $A B$ and $B C$ must exist. This means that:
- $A$ must be compatible with $B$ (i.e., the number of columns in $A$ equals the number of rows in $B$ ).
- $B$ must be compatible with $C$ (i.e., the number of columns in $B$ equals the number of rows in $C$ ).
Final Condition:
The condition under which $A (B C) = (A B) C$ holds is:
- Both $A B$ and $B C$ must exist.

Updated on:7/8/2024

|

Class 12 MATHS MATRICES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $(\to a \times \to b) \times \to c = \to a \times (\to b \times \to c)$ , where $\to a, \to b$ and $\to c$ are any three vectors such that $\to a . \to b \neq 0, \to b . \to c \neq 0$ , then $\to a$ and $\to c$ are:
Ainclined at an angle of $π / 6$
Bperpendicular
Cparallel
Dinclined at an angle fo $π / 3$
Let a, b and c are the roots of the equation $x^{3} - 7 x^{2} + 9 x - 13 = 0$ and A and B are two matrices given by $A = ⎡ ⎢ ⎣ \begin{matrix} a & b & c b & c & a c & a & b \end{matrix} ⎤ ⎥ ⎦ and B = ⎡ ⎢ ⎣ \begin{matrix} b c - a^{2} & c a - b^{2} & a b - c^{2} c a - b^{2} & a b - c^{2} & b c - a^{2} a b - c^{2} & b c - a^{2} & c a - b^{2} \end{matrix} ⎤ ⎥ ⎦$ , then the value $| A | | B |$ is equal to
A $- 154$
B $- {(154)}^{3}$
C $- 22$
D $- {(22)}^{3}$
Figure shown three points $A, B$ and $C$ in a region of unifrom electric field $\to E$ . The line $A B$ is perpendicular and $B C$ is parallel to the field lines. Then which of the following holds good. Where $V_{A}, V_{B}$ and $V_{C}$ represenet the electric potential at points $A, B$ and $C$ respectively

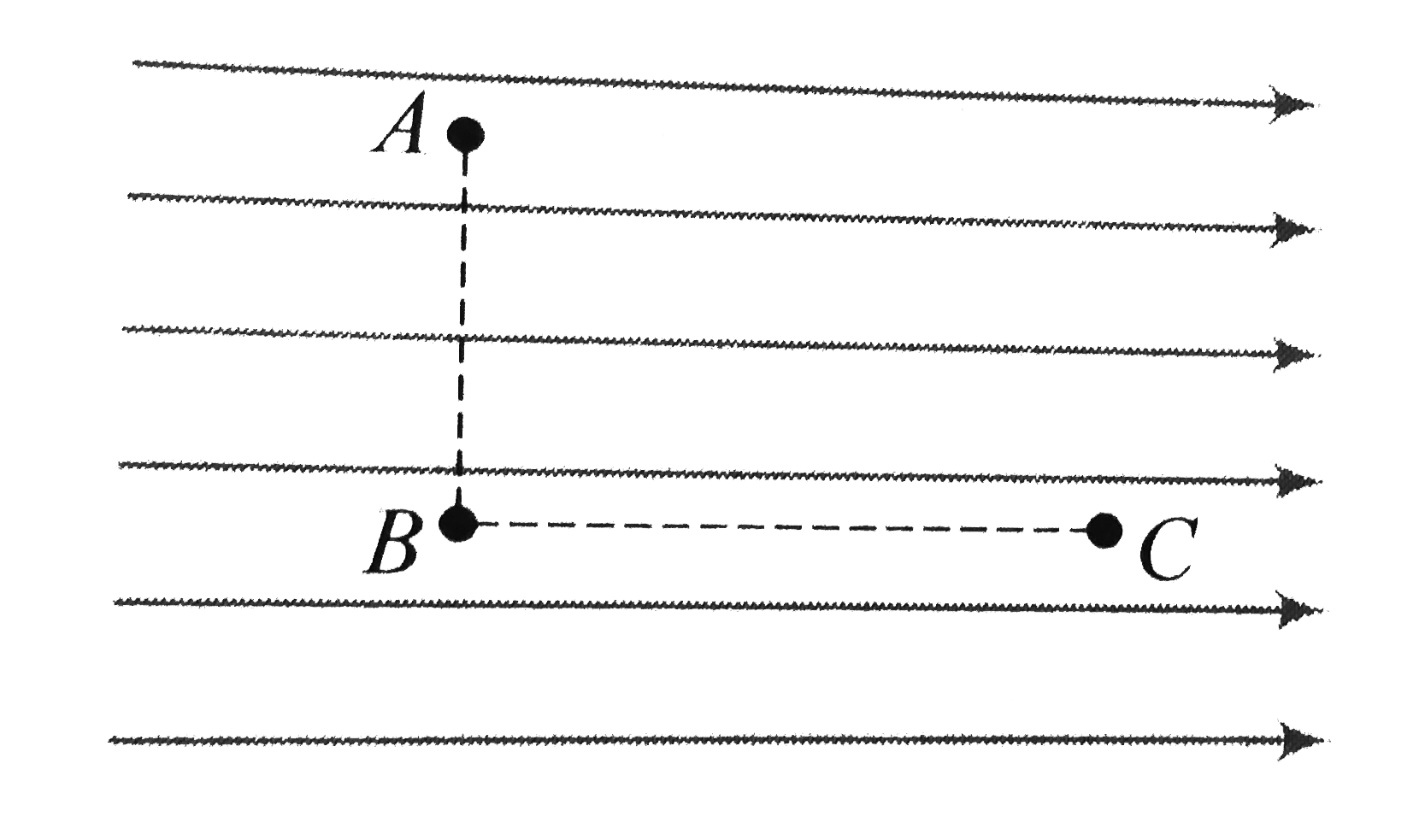A $V_{A} = V_{B} = V_{C}$
B $V_{A} = V_{B} > V_{C}$
C $V_{A} = V_{B} < V_{C}$
D $V_{A} > V_{B} = V_{C}$

NDA PREVIOUS YEARS-MATRICES & DETERMINANTS-MQS

Home
Ask Doubt
Profile