Consider the following in respect of the matrix A=(−111−1):
1. A2=−A
2. A3=4A
Which of the above is/are correct ?
1 only
2 only
Both 1 and 2
Neither 1 nor 2
The correct Answer is:B
A=[−111−1]
A.A=[−111−1][−111−1]
=[2−2−22]=−2[−111−1]
A2=−2A
A2.A=−2[−111−1][−111−1]
=−2[2−2−22]=4[−111−1]
A3=4A
Hence A2≠−A,A3=4A
Topper's Solved these Questions
Similar Questions
Consider the following inequalities in respect of any triangle ABC :
1. AC−AB<BC
2. BC−AC<AB
3. AB−BC<AC
Which of the above are correct ?
View SolutionConsider the following in respect of the matrix:
⎡⎢⎣111111111⎤⎥⎦
1. Inverse of A does not exist.
2. A3=A
3. 3A=A2
Which of the above are correct?
View Solution
Knowledge Check
Consider the following in respect of a complex number Z :
1. ¯¯¯¯¯¯¯¯¯¯¯(Z−1)=(¯¯¯Z)−1
2. ZZ−1=|Z|2
Which of the above is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2The rank of the matrix A=[12344321], is
A1B2C3D4Which one of the following is correct in respect of the matrix ?
⎡⎢⎣00−10−10−100⎤⎥⎦ ?AA. A−1 does not existBB. A=(-1) ICC. A is a Zero matrixDD. A2=1
Consider the following statements in respect of the matrix A=⎡⎢⎣012−10−3−230⎤⎥⎦
I. The matrix A is skew symmetric
II. The matrix A is symmetric
III. The matrix A is invertible
Which of the above statements is/are correct ?
View Solution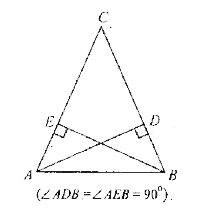
Consider the following in respect of the above figure :
1. △DAC~△EBC
2. CA/CB = CD/CE
3. AD/BE = CD/CE
Which of the above are correct ?
View SolutionConsider the following statements in respect of the set S={1,2,3…….n}:
1. (n+1)/2 is the median of the numbers in S.
2. n is the mode of the numbers in S
Which of the above statements is/are correct
View SolutionConsider the following :
1. sin1∘>sin1c
2. cos1∘<cos1c
3. tan1∘>tan1c
Which of the above are not correct ?
View SolutionConsider the following statements in respect of the matrix A=⎡⎢⎣012−10−3−230⎤⎥⎦
1. The matrix A is skew-symmetric.
2. The matrix A is symmetric.
3. The matrix A is invertible.
Which of the above statements is/are correct ?
View Solution
