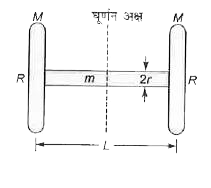
दो पतली चकती जिनमें प्रत्येक का द्रव्यमान M तथा त्रिज्या R है, एक छड़ जिसकी लम्बाई L, द्रव्यमान m तथा r त्रिज्या है, के दोनों सिरों से जुड़ी हैं। निकाय का जड़त्व आघूर्ण छड़ के केन्द्र से जाने वाले तथा इसकी लम्बाई के लम्बवत् अक्ष के परितः है
mL212+14MR2+14ML2
mL212+12mR1+24mL2
12mL2+mR22+ML212
mL212+MR2+12ML2
The correct Answer is:A
छड़ का दिए गये अक्ष के परितः जड़त्व आघूर्ण =mL212
प्रत्येक चकती का चकती के व्यास के परितः जड़त्व आघूर्ण =MR24
समान्तर अक्षों की प्रमेय से, प्रत्येक चकती का जड़त्व आघूर्ण दिए गए अक्ष के परितः
l=mL212+(MR24+ML24)
l=mL212+MR24+ML24
Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - घूर्णन गति EXERCISE - प्रश्नावली स्तर 2 प्रश्नावली एक या एक से अधिक विकल्प सही हैं6videos
घूर्णन गति
- BOOK - ARIHANT HINDICHAPTER - घूर्णन गति EXERCISE - प्रश्नावली स्तर 2 (शृंखलाबद्ध-बाधन प्रकार) अनुच्छेद-I5videos
घूर्णन गति
- BOOK - ARIHANT HINDICHAPTER - घूर्णन गति EXERCISE - प्रश्नावली स्तर 164videos
घूर्णन गति
- BOOK - ARIHANT HINDICHAPTER - घूर्णन EXERCISE - प्रश्नावली (विगत वर्षो के प्रश्न)22videos
घूर्णन
- BOOK - ARIHANT HINDICHAPTER - ठोस एवं अर्ध्दचालक युक्तियाँ EXERCISE - प्रश्नावली स्तर 2 विगत वर्षों के प्रशन9videos
ठोस एवं अर्ध्दचालक युक्तियाँ
Similar Questions
साइकिल का एक पहिया एक खुरदी सड़क पर बिना फिसले एक रेखीय चाल से चित्रानुसार चलता है, तब
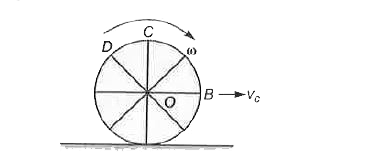 07:52View Solution
07:52View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v=rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
घड़ी की मिनट वाली सुईं की कोणीय चाल है03:23View Solutionकिसी एकसमान वृत्तीय चकती का इसके व्यास के परितः जड़त्व आघूर्ण I है। इसके तल के लम्बवत् एवं इसकी परिधि के एक बिन्दु से होकर गुजरने वाली अक्ष के परितः इसका जड़त्व आघूर्ण होगा
02:09View Solutionएक द्विपरमाणुक अणु m1 तथा m2 के दो द्रव्यमानो से बना है जोको दूरी r पर है यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकार हम इसकी घूर्णन ऊर्जा की गणना करें तब इसकी ऊर्जा दी जाएगी (n एक पूर्णांक है)
01:29View SolutionOR गेट के निर्गत को NAND गेट के दोनों निवेशों से जोड़ा जाता है। संयोजन इस भाँति कार्य करेगा
07:40View Solutionकिसी वर्ग के विपरीत शीर्षो के निर्देशांक (1,2) तथा (3,8) है , तो शीर्ष (1,2) से होकर जाने वाली रेखाओ तथा विकर्ण का समीकरण ज्ञात कीजिए ।
04:32View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
02:29View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
03:50View Solutionवृत के क्षेत्रफल में परिवर्तन कि दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए जबकि r = 3 सेमी. तथा r = 4 सेमी. है
04:26View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
05:19View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:06View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
04:25View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
06:39View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
53:00View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
02:36View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
02:42View Solution

