Question

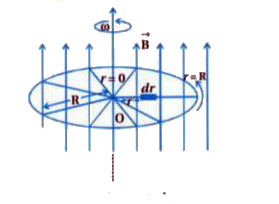
A wheel having n conducting concentric spokes is rotating about it geometrical axis with an angular velocity $\omega$, in a uniform magnetic field B perpendicular to its plane prove that the induced emf generated between the rim of the wheel and the center is $\frac{\omega B{R}^2}{2}$, where R is the radius of the wheel. It is given that the rim of the wheel is conducting.

Explanation

Consider a small element dr on any spoke at a distance r from the center.
Linear velocity of this element `v = romega`, emf induced in a small element dr is,
`d epsilon = Bvl`
`=B(r omega)dr`
Total emf induced along the entire length of any spoke is ,
`epsilon =int_0^R B omega r dr`
`therefore epsilon = B omega int_0^R r dr`
`therefore epsilon =Bomega[r^2/2]_0^R`
`therefore epsilon =Bomega [R^2/2-0^2/2]`
`therefore epsilon =(BomegaR^2)/2` which is proved.
Now according to right hand screw rule with equation `vecF = -e(vecv xx vecB)` shows that free electrons in a spoke will experience force towards the center of the wheel therefore, the free electrons accumulate at the center of the wheel leaving the rim positively charged. So it act as battery with emf will be `(BomegaR^2)/2`.
Here voltage obtained from all spokes are parallel so the resultant emf will be `(BomegaR^2)/2`.