Deduce an expression for the electric field E due to a dipole of length '2a' at a point distant 'r' from the centre of the dipole on the axial line.
(b) Draw a graph of E versus r for r>>a.
©
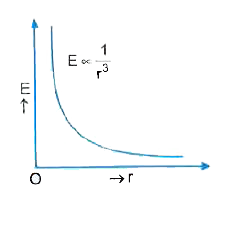
E-r graph for r>>ashown in figure
 The positions of stable and unstable equilibrium have represented in in Both positions , torque acting on the dipole is zero.
The positions of stable and unstable equilibrium have represented in in Both positions , torque acting on the dipole is zero.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A)
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A) (FILL IN THE BLANKS)
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -I
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
Similar Questions
(a) Derive an expression for the elecrtric field E due to a dipole of length '2a at a point
distant r from the centre of the dipole on the axial line.
(b) Draw a graph of E versus r for r >>a.
(c) If the diploe were kept in a uniform external electric fields E0 Diagrammatically represent
the position of the dipole in stable and unstable equilibrium and write the expressions
for the torque acting on the dipole in both the cases.
View SolutionA short electric dipole has dipole moment of 4×10−9Cm. Determine the electric potential due to the dipole at a point distant 0.3 m from the centre of the dipole situated on (a) the axial line (b) on equatorial line and (c) on a line making an angle of 60∘ wth the dipole axis.
View Solution
Knowledge Check
The electric field due to a dipole at a distance r from its centre is proportional to
A1r3Br3Cr2D1r2Electric field intensity (E) due to an electric dipole varies with distance (r) from the point of the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3
An electric dipole of dipole moment →p consists of point charges +q and -q separated by a distance '2a' apart. Deduce the expression for the electric field →E due to the dipole on its axial line in term of the dipole moment →p. Hence show that in the limit r>>a,→E=2→p4π∈0r3
(b) Given the electric field in the region →E=2xˆi Find the net electric flux through the cube and the charge enclosed by it.
View SolutionDraw a graph of electric field E(r) with distance r from the centre of the shell for 0≤r≤0 .
View SolutionElectric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
View SolutionElectric field intensity (E) due to an electric dipole varies with distance (r) of the point from the center of dipole as :
View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View Solution
