Obtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each 100 pF capacitor.
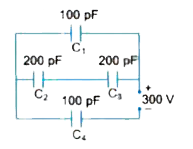
The arrangement is redrawn in Fig. Here C2andC3 are in series, hence their combinaed capacitance C. will be
C.=C2C3C2+C3=200×200200+200pF=100pF
Now this combination C. is in parallel arrangement to C1, hence their combined capacitance
C..=C.+C1=100+100pF=200pF
Finally C" is in series with C4, hence resultant capacitance C will be
C=C..C4C..+C4=200×100200+100pF=2003pF
∴ Total charge on whole arrangement
Q=CV=2003pF×300V
=2×104pC=2×10−8C
∴ Charge on combination C.. = Charge on C4=2×10−8C
If potential difference across C.. and C4 be V.. and V4 respectively, then
V..+V4=300VandV..V4=C4C..=100pF200pF=12
⇒V..=100VandV4=200V
In the arrangement C.., C1 and C. are in parallel, hence
V1=V.=V..=100V
∴Q1=C1V1=100pF×100V=104pC=10−8C
As in the arrangement C., capacitors C2andC3 are connected in series and
C2=C3, hence V2=V3=V.2=100V2=50V
∴Q2=Q3=C.V.=100pF×100V=104pC=10−8C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Obtain equivalent capacitance of the following network, Fig. For a 300V supply determine the charge and voltage across each capacitor.
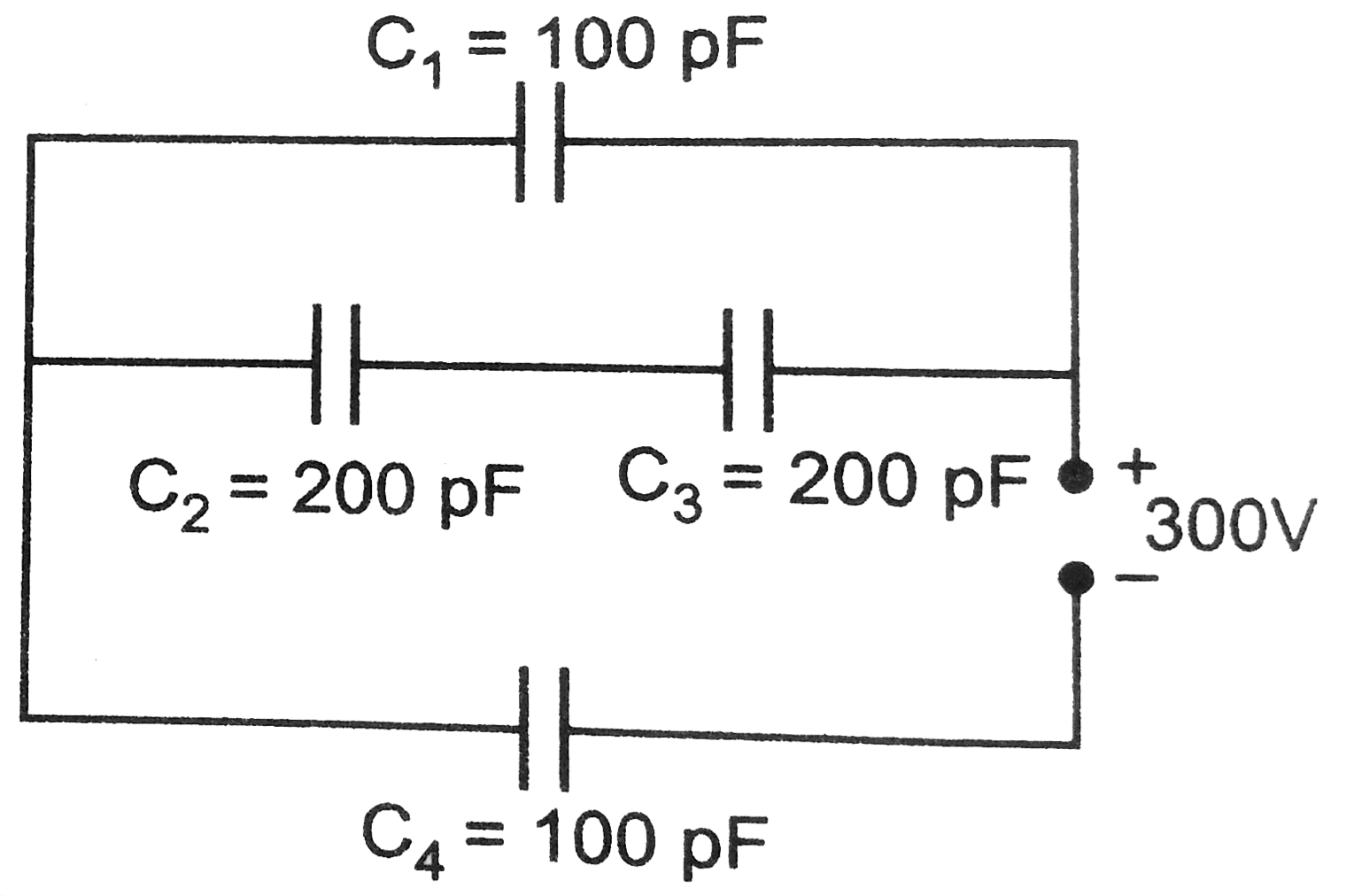
View SolutionObtain equivalent capacitance of the following net work, Fig. For a 300V supply determine the charge and voltage across each capacitor.

View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

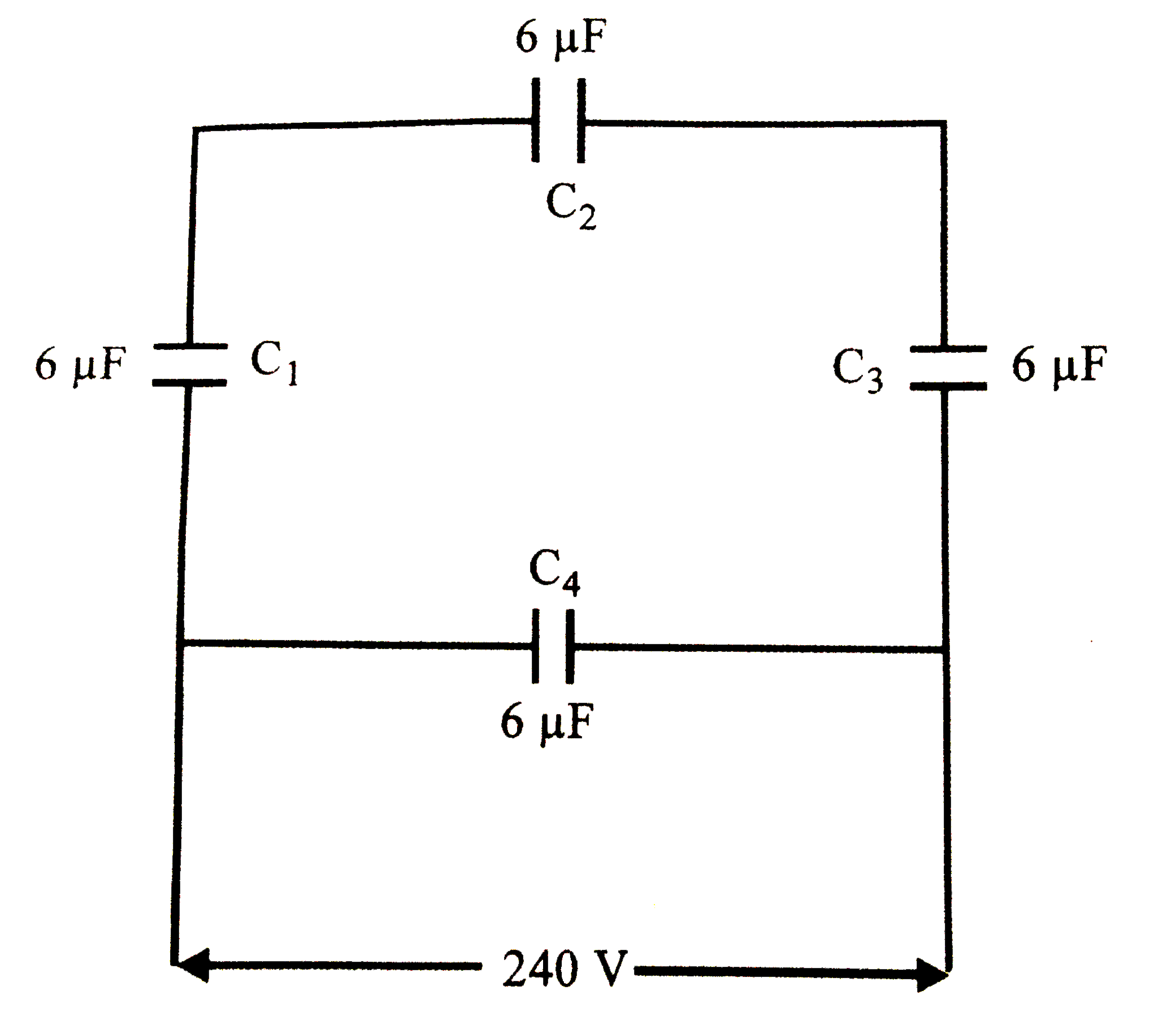
View SolutionA network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
View SolutionFind the equivalent capacitance of the network shown in the fig , when each capacitor is of 1 μF . When the ends X and Y are connected to a 6 V battery , find out (i) the charge and (ii) the energy stored in the network

View SolutionThree capacitors of capacitance 2pF,3pFand4pF are connected in parallel. (a) what is the total capacitance of the combination ? (b) Determine the charge on each capacitor, If the combination is connected to 100V supply.
View SolutionThree capacitors of capacitance 2pF,3pFand4pF are connected in parallel. (a) what is the total capacitance of the combination ? (b) Determine the charge on each capacitor, If the combination is connected to 100V supply.
View SolutionThree capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination ?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
View SolutionA 12pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ? If another capacitor of 6pF is connected across the combination, find the charge stored and potential difference across each capacitor.
View Solution
