(a) Determine the 'effective focal length' of the combination of the two lenses in Exercise 9.10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident ? Is the notion of effective focal length of this system useful at all ? <> (b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens system, and the size of the image.

Text Solution

Verified by Experts

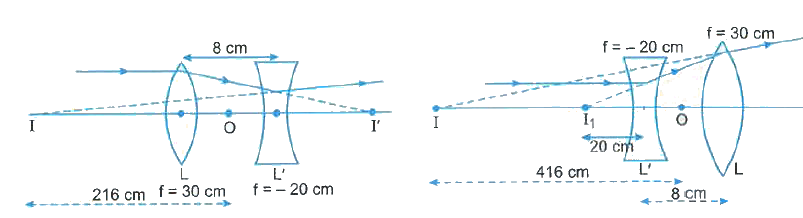
(a) Let a parallel beam be incident first on convex lens of focal length l= 30 cm. Naturally, the beam will get focused at a point l 30 cm behind convex lens, in the absence of concave lens. However, the image Ix behaves as a virtual object for concave lens, of focal length 20 cm, which is placed 8.0 cm from convex lens. Thus, for concave lens u. = 30 - 8 = 22 cm
$∴ \frac{1}{v} . - \frac{1}{+ 22} = \frac{1}{- 20} \Rightarrow \frac{1}{v^{.}} = - \frac{1}{20} + \frac{1}{22} \Rightarrow v^{.} = - 220 c m$
Thus, an incident parallel beam will appear to diverge from a point I, 220 cm from concave lens (or 216 cm from centre point O of the two lens system).
Then let us consider that a parallel beam of light is incident first on the concave lens [Fig. 9.09]. The beam will appear to diverge from a point lv 20 cm behind concave lens, in the absence of convex lens. lx now behaves as a real object for convex lens of focal length 30 cm. Thus, for convex lens u. = - (20 + 8) = - 28 cm
$∴ \frac{1}{v^{.}} - \frac{1}{- 28} = \frac{1}{+ 30} \Rightarrow \frac{1}{v^{.}} = \frac{1}{30} + \frac{1}{- 28}$
$\Rightarrow v . = - 420 c m$
Thus, the incident parallel beam will appear to diverge from a point I, 420 cm behind convex lens (or 416 cm from centre point O of the two lens system).
Thus, it is clear that there is no fixed answer for effective focal length of the combination.
(b) Given that h = 1.5 cm and distance of object from convex lens (f = + 30 cm), u = - 40 cm

$∴ \frac{1}{v} - \frac{1}{- 40} = \frac{1}{30} \Rightarrow \frac{1}{v} = \frac{1}{30} - \frac{1}{40} = \frac{1}{120} \Rightarrow v = 120 c m$
Hence, for concave lens $u . = + (120 - 8) = + 112 c m$ and $f . = - 20 c m$
$∴ \frac{1}{v_{2}} - \frac{1}{+ 112} = \frac{1}{- 20} \Rightarrow \frac{1}{v} = \frac{1}{112} - \frac{1}{20} \Rightarrow v_{2} = - 24.3$ cm
Thus, a real image is formed 24.3 cm behind concave lens.
Hence, magmfication produced by convex lens $| m_{1} | = \frac{v}{u} = \frac{120}{40} = 3$
and magnification produced by concave lens $| m_{2} | = \frac{24.3}{112} = 0.22$
$∴$ total magnification of image $| m | = | m_{1} | \times | m_{2} | = 3 \times (0.22) = 0.66$
$∴$ Size of image $h . = m h = 0.66 \times 1.5 = 1$ cm

Updated on:21/07/2023

The focal length of the combination of two thin lenses in contact is 80 cm. If the focal length of one lens is -20 cm, what is the power of the other lens ?
A2.25 D
B6.25 D
C $- 2.5$ D
D $- 3.75$ D