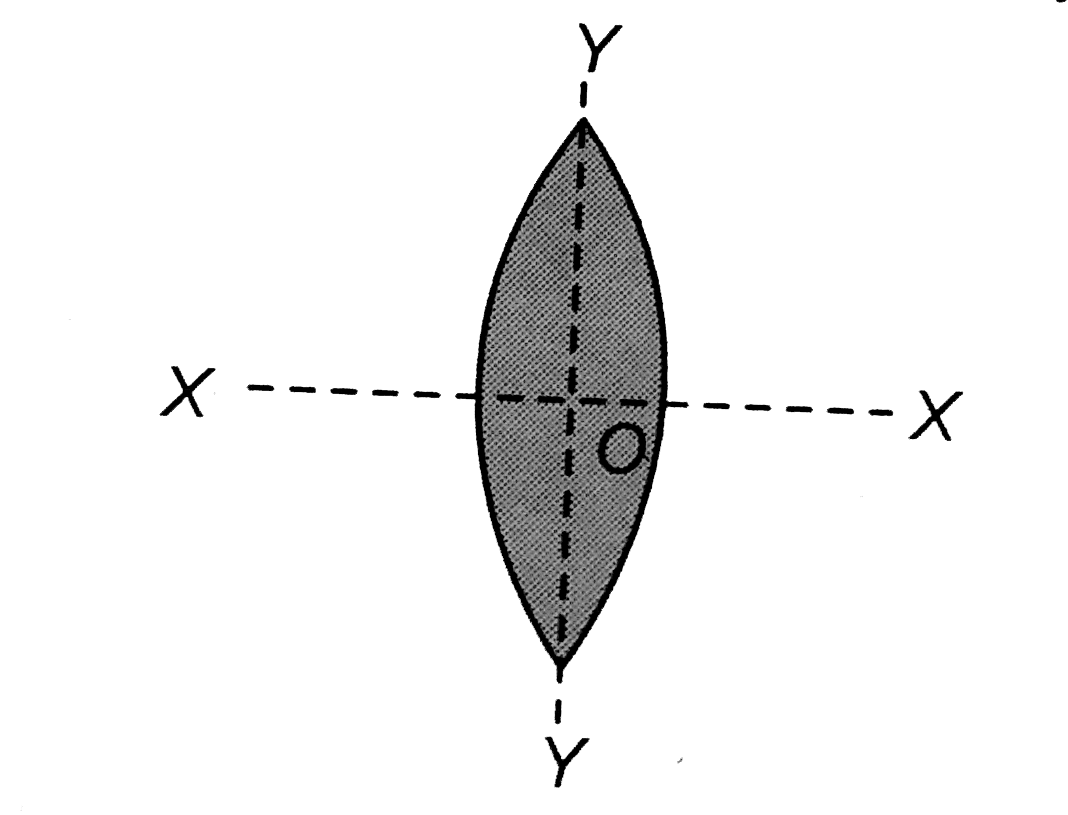
An equiconvex lens is cut into 2 halves along (i) XOX' and (ii) YOY'' as shown in the Fig. Let and be the focal lengths of the complete lens, of each half in case (i) and of each half in case (ii) respectively, then

The correct Answer is:D
Here
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:FILL IN THE BLANKS
Explore 20 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:TRUE OR FALSE
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:U-LIKE SERIESChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:CASE BASED/SOURCE- BASED INTEGRATED QUESTIONS
Explore 19 Videos
- NUCLEIBook:U-LIKE SERIESChapter:NUCLEIExercise:Self Assessment Test
Explore 10 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:U-LIKE SERIESChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:SECTION B
Explore 1 Video
Similar Questions
An equiconvex lens is cut into two halves along (i)XOX′ and (ii)YOY′ as shown in the figure. Let f,f′f'' be the focal lengths of the complete lens, of each half in case (i), and of each half in case (ii), respectively
Choose the correct statement from the following
View SolutionIf f(V) and fR are the focal lengths of a convex lens for violet and red light respectively and FVand FR are the focal lengths of concave lens for violet and red light respectively, then we have
View Solution
Knowledge Check
An equiconvex lens is cut into two halves along (i)XOX′ and (ii)YOY′ as shown in the figure. Let f,f′f'' be the focal lengths of the complete lens, of each half in case (i), and of each half in case (ii), respectively
Choose the correct statement from the following
 Af′=2f,f''=fBf′=f,f''=fCf′=2f,f''=2fDf′=f,f''=2f
Af′=2f,f''=fBf′=f,f''=fCf′=2f,f''=2fDf′=f,f''=2fTwo thin lenses of focal lengths f1andf2 are placed in contact. The focal length of the composite lens will be
Af1+f22Bf1+f2f1f2C√f1f1Df1f2f1+f2Let fv and fr are the focal lengths of a convex lens for violet and red lights respectively. If Fv and Fr are the focal lengths of a concave lens for violet and red light respectively, then
Afv<fr and Fv>FrBfv<fr and Fv<FrCfc>fr and Fv>FrDfv>fr and Fv<Fr
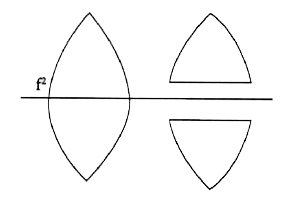
The figure shows and equiconvex lens of focal length f. It the lens is cut along PQ, the focal length of each half will be

View SolutionIf a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
View SolutionIf f(V) and fR are the focal lengths of a concex lens for violet and red light respectively and FVand FR are the focal lengths of concave lens for violet and red light respectively, then we have
View SolutionfB and fR are focal lengths of a convex lens for blue and red light respectively and F_(B_ and Fr are the focal lengths of the concave lens for blue and red light respectively. We must then have
View SolutionThe figure shows and equiconvex lens of focal length f. It the lens is cut along PQ, the focal length of each half will be

View Solution
