A function f is defined on an interval [a, b]. Which of the following statement(s) is are incorrect? (A) If f(a) and f(b) have opposite signs,then there must be a point c∈(a,b) such that f(c)=0.
Step by step video & image solution for A function f is defined on an interval [a, b]. Which of the following statement(s) is are incorrect? (A) If f(a) and f(b) have opposite signs,then there must be a point cin(a,b) such that f(c)=0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Consider a real valued continuous function f(x) defined on the interval [a, b). Which of the followin statements does not hold(s) good? (A) If f(x)≥0 on [a, b] then ∫baf(x)dx≤∫baf2(X)dx (B) If f (x) is increasing on [a, b], then f2(x) is increasing on [a, b]. (C) If f (x) is increasing on [a, b], then f(x)≥0 on (a, b). (D) If f(x) attains a minimum at x = c where a<c<b, then f'(c)=0.
View SolutionLet f be a differentiable function on the open interval(a, b). Which of the following statements must be true?
(i) f is continuous on the closed interval [a,b],
(ii) f is bounded on the open interval (a,b)
(iii)If a < a1< b1 < b, and f(a1) < 0 < f(b1), then there is a number c such that a1 < c < b, and f(c) = 0
(a)Only I and II
(b)Only I and III
(c)Only II and III
(d)Only III
View Solution
Knowledge Check
A function f:A→B is defined as :
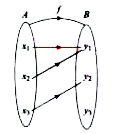
Which of the following is true ?Aone - one functionBone-one and onto functionCmany - one and into functionDmany-one and onto functionIf f is an odd function and f(a)=b, which of the following must also be true ?
I. f(a)=−b
II.f(−a)=b
III. f(−a)=−bAonly IBOnly IIICOnly IIIDOnly I and II
The function f(x) is defined on the interval [0,1]. What are the domains of definition of functions.
(a) f(sinx),(b)f(2x+3)?
View SolutionLet f be a differentiable function on the open interval(a, b). Which of the following statements must be true? (i) f is continuous on the closed interval [a,b],(ii) f is bounded on the open interval (a,b)
View SolutionLet fandg be function continuous in [a,b]and differentiable on [a,b].If f(a)=f(b)=0 then show that there is a point c∈(a,b) such that g'(c)f(c)+f'(c)=0.
View SolutionLet fandg be function continuous in [a,b]and differentiable on [a,b].If f(a)=f(b)=0 then show that there is a point c∈(a,b) such that g'(c)f(c)+f'(c)=0.
View SolutionLet f be continuous on [a, b] and assume the second derivative f" exists on (a, b). Suppose that the graph of f and the line segment joining the point (a,f(a))and(b,f(b)) intersect at a point (x0,f(x0)) where a<x0<b. Show that there exists a point c∈(a,b) such that f(c)=0.
View SolutionThe function f(x) is defined on the interval (0,1). What are the domains of definition of the following functions.
(a) f(3x2),(b)f(x−5),(c)f(tanx)?
View Solution
