A particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
−3GMa
−2GMa
−GMa
−4GMa
The correct Answer is:A

Here, mass of the particle=M
Mass of the spherical shell=M
Radius of the spherical shell = a
Point P is at a distance a/2 from the centre of the shell as shown in figure. Gravitational potential at point P due to particle at O is
V1=−GM(a/2)
Gravitational potential at point P due to spherical shell is
V2=−GMa
Hence, total gravitational potential at the point P is
V=V1+V2=−GM(a/2)+(−GMa)
=−2GMa−GMa=−3GMa
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - CHECK YOUR NEET VITALS25videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)11videos
BEHAVIOUR OF PERFECT GAS AND KINETIC THEORY
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs31videos
KINEMATICS
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View Solution
Knowledge Check
- Question 1 - Select One
A particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
A−GMRB−3GMRC−2GMRDzero - Question 2 - Select One
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmR - Question 3 - Select One
P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
A−GMrB−GMaC−GMra2D−GM(a−ra2)
A mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is:
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
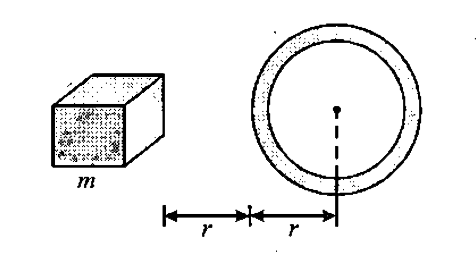 View Solution
View SolutionA hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
View Solution

