Let $α$ and $β$ be the roots of the quadratic equation $a x^{2} + b x + c = 0$ , observe the lists given below :
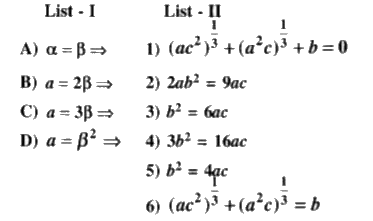The correct match is

A

$\begin{matrix} A & B & C & D \\ 5 & 2 & 4 & 6 \end{matrix}$

B

$\begin{matrix} A & B & C & D \\ 5 & 2 & 1 & 4 \end{matrix}$

C

$\begin{matrix} A & B & C & D \\ 5 & 4 & 2 & 6 \end{matrix}$

D

$\begin{matrix} A & B & C & D \\ 5 & 2 & 4 & 1 \end{matrix}$

Text Solution

Verified by Experts

The correct Answer is:D

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $α, β$ are the roots of the quadratic equation $a x^{2} + b x + c = 0 and 3 b^{2} = 16 a c$ , then
A $α = 4 β or β = 4 α$
B $α = - 4 β or β = - 4 α$
C $α = 3 β or β = 3 α$
D $α = - 3 β or β = - 3 α$
Question 2 - Select One
If $α$ and $β$ are the roots of the quadratic equation $x^{2} + b x - c = 0$ , then the equation whose roots are b and c, is
A $x^{2} + α x - β = 0$
B $x^{2} - [(α + β) + α β] x - α β (α - β) = 0$
C $x^{2} + [(α + β) + α β] x + α β (α + β) = 0$
D $x^{2} + [(α + β) + α β] x - α β (α + β) = 0$
Question 3 - Select One
If $α and β$ are the roots of the quadratic equation $a x^{2} + b x + 1$ , then the value of $\frac{1}{α} + \frac{1}{β}$ is
Aa
B $- a$
Cb
D $- b$

AAKASH SERIES-QUADRATIC EQUATIONS & EXPRESSIONS-PRACTICE EXERCISE

Home
Ask Doubt
Profile