The first three terms of an A.P. are 3y−1,3y+5,and5y+1. Find y.Solution in Kannada
The correct Answer is:y=5
Step by step video, text & image solution for The first three terms of an A.P. are 3y -1, 3y + 5, and 5y+ 1. Find y. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TO FIND THE NTH TERM OF AN A.P. (ILLUSTRATIVE EXAMPLES)11videos
ARITHMETIC PROGRESSIONS
- BOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ARITHMETIC SERIES (ILLUSTRATIVE EXAMPLES)6videos
ARITHMETIC PROGRESSIONS
- BOOK - ZEN PUBLICATIONCHAPTER - AREA RELATED TO CIRCLES EXERCISE - ADDITIONAL QUESTIONS (HIGHER ORDER THINKING SKILLS)7videos
AREA RELATED TO CIRCLES
- BOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)9videos
CIRCLES
Similar Questions
How many two digit numbers are divisible by 3?
01:32View SolutionFind the sum of all two digit natural numbers which when divided by 3 yield 1 as remainder.
01:30View SolutionFind the area of the shaded region portion in the given figure if E is the midpoint of AB,AGE and BEF are quadrants, and DOC is a semicircle.
 00:52View Solution
00:52View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
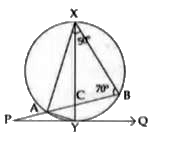 03:39View Solution
03:39View SolutionThe first three terms of an A.P. respectively are 3y−1, 3y+5 and 5y+1 . Then, y equals (a) −3 (b) 4 (c) 5 (d) 2
01:11View Solutionx+5y=15;2x-3y=1
04:00View Solution(3y-8)xx(5y-1)
02:28View SolutionIf 3y+112+6(4−5y)=12, then y = _____
04:29View Solution((y^(3)-3y^(2)+5y-1)/(y-1))
04:13View Solutionआव्यूह विधि से निम्नलिखित समीकरण निकायों को हल कीजिये
4x−3y=53x−5y=101:52View SolutionThe first three terms of an A.P. respectively are 3y−1, 3y+5 and 5y+1 . Then, y
equals
(a) −3 (b) 4 (c) 5 (d) 204:08View SolutionFind , whether or not the first polynomial is a factor of the second: x+1, 2x2+5x+4 y−2, 3y3+5y2+5y+2
04:43View SolutionFind the coefficient of :
y5 in (3y2+13y)1002:19View SolutionFind the product: 3y^2*5y^3*y
01:35View SolutionFind the quotient and remainder (4x^5y ^5– 2x^3y^3 + 6x^3y^5) div (-2x^3y^3)
02:44View Solution
