Write first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10
(ii) a=-2, d=0
(iii) a=4, d=−3
(iv) a=−1,d=12
(v) a=−1.25,d=−0.25 Solution in Kannada
The correct Answer is:In these problems, we add the common difference to each preceding term to get the next term.
Step by step video, text & image solution for Write first four terms of the AP, when the first term a and the common difference d are given as follows: (i) a=10, d=10 (ii) a=-2, d=0 (iii) a=4, d=-3 (iv) a=-1, d=1/2 (v) a=-1.25, d= -0.25 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TEXTUAL EXERCISE (Exercise 1.2)
20 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - TEXTUAL EXERCISE (Exercise 1.3)
20 Videos
- ARITHMETIC PROGRESSIONSBOOK - ZEN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - ARITHMETIC SERIES (ILLUSTRATIVE EXAMPLES)
6 Videos
- AREA RELATED TO CIRCLES BOOK - ZEN PUBLICATIONCHAPTER - AREA RELATED TO CIRCLES EXERCISE - ADDITIONAL QUESTIONS (HIGHER ORDER THINKING SKILLS)
7 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
Similar Questions
Fill in the blanks in the following table, given that a is the first term, d the common difference and an nth term of the AP :

View SolutionFind the sum of the following Aps:
(i) 2, 7, 12, …….., to 10 terms.
(ii) −37,−33,−29, …….., to 12 terms.
(iii) 0.6, 1.7, 2.8,….., to 100 terms
(iv) 115,112,110,……,to 11 terms
View SolutionFind the sum of all two digit natural numbers which when divided by 3 yield 1 as remainder.
View SolutionFind the area of the shaded region portion in the given figure if E is the midpoint of AB,AGE and BEF are quadrants, and DOC is a semicircle.

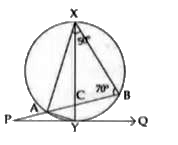
View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:(i) a = 10, d= 10
(ii) a = –2, d = 0
(iii) a = 4, d = – 3
(iv) a = – 1, d = 1/2
(v) a = – 1.25, d = – 0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows: a) a=10, d=10 (b) a=-2. d=0 (c) a=4, d=-3 (d) a=-1, d=3 (e) a=-1.25, d=-0.25 :
View Solutionदी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अंतर d निम्नलिखित है:
(i)a=10,d=10(ii)a=−2,d=0
(iii)a=4,d=−3(iv)a=−1,d=13
(v)a=−1.25,d=−0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:
(v) a = -1.25, d = -0.25.
View SolutionWrite first four terms of the A.P , when the first term a and the common difference d are given as follows:
(i) a=10,d=10
(ii) a=−2,d=0
(iii) a=4,d=3.
(iv) a=−1,d=12.
(v) a=−1.25,d=−0.25.
View Solutionदी हुई A.P. के प्रथम चार पद लिखिए :
a=10, d=10
a=−2,d=0<br>a=4,d=−3
a=-1,d=12
a=-1.25,d=-0.25
View Solutionदी हुई A.P. के प्रथम चार पद लिखिए जवकि प्रथम पद तथा सार्व अन्तर d निम्नलिखित है।
(I)a=10,d=10
(ii)a=−11,d=12
(iii) a=−1,d=−0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10
(ii) a=-2, d=0
(iii) a=4, d=−3
(iv) a=−1,d=12
(v) a=−1.25,d=−0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10
(ii) a=-2, d=0
(iii) a=4, d=−3
(iv) a=−1,d=12
(v) a=−1.25,d=−0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10
(ii) a=-2, d=0
(iii) a=4, d=−3
(iv) a=−1,d=12
(v) a=−1.25,d=−0.25
View SolutionWrite first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a=10, d=10
(ii) a=-2, d=0
(iii) a=4, d=−3
(iv) a=−1,d=12
(v) a=−1.25,d=−0.25
View Solution
