From the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base of the original cone. Find the total surface area of the remaining solid. [use π=3.14,√5=2.236]Solution in Kannada
The correct Answer is:350.3cm2.
Step by step video, text & image solution for From the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base of the original cone. Find the total surface area of the remaining solid. [use pi=3.14,sqrt(5)=2.236] by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS - LONG ANSWER [LA] TYPE-QUESTIONS
18 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
11 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -SHORT ANSWER [SA] TYPE-1 QUESTIONS
16 Videos
- STATISTICS BOOK - ZEN PUBLICATIONCHAPTER - STATISTICS EXERCISE - ZEN ADDITIONAL QUESTIONS IIT FOUNDATION
5 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
10 Videos
Similar Questions
The surface areas of a cube and a sphere are equal. Prove that the ratio of their volumes is √π6:1.
View SolutionA sector of a circular is of radius 12 cm and angle 120∘. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
View SolutionFind the ratio of volumes of a cube to that of a sphere which exactly fits inside the cube.
View SolutionThe mean of five numbers is 18. If one number is excluded then their mean is 16. Find excluded number.
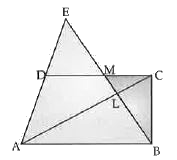
View SolutionThrought the mid-point M of the sides of a parallelogram ABCD, the line BM is drawn intersecting AC at L, and AD produced to E. Prove that EL=2BL.
View SolutionIn Fig. 16.74, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use π=22/7 and √5=2.236) (FIGURE)
View Solutionएक शंकु की ऊंचाई 16 cm है आधार की त्रिज्या 12 cm है |
इस शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
(π=3.14 का प्रयोग कीजिए)
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View Solutionएक ठोस शंकु की ऊँचाई 12 सेमी तथा वृत्ताकार आधार का क्षेत्रफल 64π(सेंटीमीटर)2 है। इसके आधार के समान्तर एक समतल के द्वारा इसके शीर्ष से 9 सेमी. दुरी से काटकर नया शंकु बनाया जाता है तो , इस शंकु के आधार का क्षेत्रफल होगा:
View SolutionWhat will be the height of the cone of radius 12 cm if a solid cone is made by melting a solid coneof radius of base 6 cm and of slant height 10 cm ?
View Solutionएक शंकु की ऊँचाई 16 सेमी है और आधार की त्रिज्या 12 सेमी है | इस शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात करें | (π=3.14 लें |)
View Solutionएक शंकु की ऊँचाई 16 cm है, और आधार की त्रिज्या 12 cm है । इस शंकु का वक्रपृष्ठीय क्षेत्रफल एवं सम्पूर्ण क्षेत्रफल ज्ञात कीजिए । (π = 3.14 का प्रयोग कीजिए ।)
View Solutionएक शंकु की ऊँचाई 16 सेमी है, और आधार की त्रिज्या 12सेमी है| इस शंकु का वक्रपृष्ठीय क्षेत्रफल एवं सम्पूर्ण क्षेत्रफल ज्ञात कीजिए | (π=3.14 का प्रयोग कीजिए )
View SolutionThe height of a cone is 16 cm and the radius of the base is 12 cm. Find the curved surface area of this cone. ( pi= 3.14 Use)
View SolutionIn Figure, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use π=22/7 and √5=2.236)
View Solution
