inside the circles x2+y2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to
Step by step video & image solution for inside the circles x^2+y^2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Inside the unit circle S=x^2+y^2=1, there are three smaller circles of equal radius a, touches to each other and also touches to S. The value of 'a' equals
View SolutionInside the unit circle S={(x,y)∣x2+y2=1} there are three smaller circles of equal radius a ,touches to each other and also touches to S. The value of a equals
View Solution
Knowledge Check
Inside the circle S:x2+y2=4, there are 3 smaller circles of equal radius a, tangent to each other and to S. The value of a equals.
A2√2(√2−1)B2√3(2−√3)C2√2(2−√3)D2√3(√3−1)Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2
Three circles of equal radius 'a' cm touch each other. The area of the shaded region is :
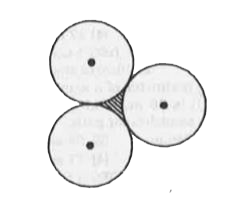
View SolutionThree circles of equal radius 'a' cm touch each other. The area of of the shaded region is :

View SolutionConsider the circles x2+(y−1)2=9,(x−1)2+y2=25. They are such that these circles touch each other one of these circles lies entirely inside the other each of these circles lies outside the other they intersect at two points.
View SolutionConsider the circles x2+(y−1)2=9,(x−1)2+y2=25. They are such that these circles touch each other one of these circles lies entirely inside the other each of these circles lies outside the other they intersect at two points.
View SolutionIf one of the diameters of the circle x2+y2−2x−6y+6 =0 is a chord to the circle with centre at (2,1) then the radius of the circle is equal to.
View SolutionIn the following diagram there are three circles packed in another circle, such that each circle is tangent to all other circles in this arrangement. The radius of the circumscribing circle A is 1 cm, and circle B and circle C are congruent. Find the radius of the circle D.

View Solution
