एक समान रेखिक घनत्व वाले ऊधर्वाधर डोरी के निचले सिरे पर गुटका M लटका हुआ है। डोर का दूसरा सिरा दृढ आधार (बिन्दु O) से संलगन है। तरंगदैध्र्य λ0 की अनुप्रस्थ तरंग स्पन्द (स्पन्द 1) बिन्दु O पर उतपन्न की गई है। ये तरंग स्पंद बिन्दु O से बिन्दु A तक TOA समय में पहुँचती है। गुटके M को बिना विक्षोमित किये हुए बिन्दु A पर निर्माण की गई तरंग दैध्र्य λ0 की अनुप्रस्थ तरंग स्पंद (स्पंद 2) बिन्दु A से बिन्दु O तक TAo समय में पहुँचती है। निम्न में कोनसा (से) कथन सही है/हैं
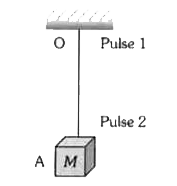
डोर के मध्य बिन्दु पर स्पंद 1 एवं स्पंद 2 का वेग समान है
डोर के अनुदिश प्रोषित किसी भी स्पंद का वेग उसकी आवृत्ति एवं तरंग-दैध्र्य पर निर्भर नहीं है
स्पंद 1 की तरंग-दैध्र्य बिन्दु A तक पहुंचने में लम्बी हो जाएगी
सयम TAo=TOA
The correct Answer is:B, D
V=√Tμ अतः किसी भी स्थिति में दो स्प्नदो की चल समान
होगी, इसलिये दोनों स्प्नदो द्वारा लिया समय समान होगा।
λf=v⇒λ=Vf⇒λ∝V, जब स्पन्द 1,A पर पहुंचेगा तो
उसकी चल घटेगी इसलिए तरंगदैध्र्य λ घटेगा
नॉट : यदि हम केवल वेग के परिमाण को माने तो विकल्प (A, B, D) सही होने अन्यथा केवल (B, D) विकल्प सही होंगे
Topper's Solved these Questions
- ध्वनि एवं तरंगBOOK - ERRORLESS HINDICHAPTER - ध्वनि एवं तरंगEXERCISE - प्राक्क्थन एवं कारण
25 Videos
- ध्वनि एवं तरंगBOOK - ERRORLESS HINDICHAPTER - ध्वनि एवं तरंगEXERCISE - SELF EVALUATION TEST
19 Videos
- ध्वनि एवं तरंगBOOK - ERRORLESS HINDICHAPTER - ध्वनि एवं तरंगEXERCISE - ग्राफीय प्र्शन
6 Videos
- धारा विद्युतBOOK - ERRORLESS HINDICHAPTER - धारा विद्युतEXERCISE - Self Evaluation Test
20 Videos
- न्यूटन के गति के नियम BOOK - ERRORLESS HINDICHAPTER - न्यूटन के गति के नियम EXERCISE - Self evaluation
16 Videos
Similar Questions
प्रक्क्थन : चन्द्रमा की सतह पर दो व्यक्ति एक दूसरे से बात नहीं कर सकते है।
कारण : चन्द्रमा पर वायुमण्डल नहीं है।
View Solutionएक इंजन नियत चाल से वृतीय पथ पर गतिमान है। यदि इंजन सिटी बजाकर 500Hz आवृत्ति की ध्वनि उतपन्न करता हे। तो चित्र में दिखाए अनुसार पथ के केन्द्र पर खड़ा हुआ एक व्यक्ति है द्वारा प्रेक्षित आवृत्ति होगी

View Solutionn आवृत्ति से कम्पन्न करने वाले स्रोत द्वारा उतपन्न दोऐ में तरंगे किसी क्षण दोयी और संचरित हो रही है
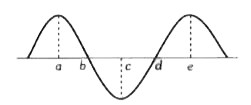
निम्न कथन पर विचार करे
(I) तरंग की चाल 4n×ab है
(II) बिन्दु a व d पर माध्यम 43n बाद समन कला में होंगे
(III) बिन्दु b तथा e के बीच कलान्तर 3π2
इनमे सत्य कथन है
View Solutionचित्र में एक ताप वैद्युत युग्म द्वारा उत्पन्न सूक्ष्म वि. वा. बल को मापने के लिए प्रयुक्त विभवमापी को दिखाया गया है। मीटर तार PQ का प्रतिरोध 5Ω एवं ड्रायवर सैल (मानक) का वि. वा. बल 2 V है। जब 6.00 mV के वि. वा. बल का मापा जाता है तो PQ के अनुदिश संतुलन बिन्दु 0.600 m पर प्राप्त होता है, प्रतिरोध R का मान है

View Solutionएक कार एक समान वेग से घर्षणयुक्त सड़क पर गतिमान है। न्यूटन की गति के प्रथम नियमानुसार
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionकिसी बिन्दु पर संतत फलन होता है -
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
View Solutionबिन्दु (-1,0) से होकर जाने वाले और y-अक्ष को (0,2) पर स्पर्श करने वाला वृत्त निम्न बिन्दु से भी होकर जाता है ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionबिन्दु (1, 2) से दीर्घवृत्त 3x2+2y2=5 पर खींची गई स्पर्शी युग्मों के बीच का कण है
View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
View Solution
