A bus accelerates from rest at a constant rate α for some time,after which it decerates at a constant rate β to come to rest.If the total time elapes is t seconds then ,evaluate.
(a)the maximum velocity achieved and
(b)the total distance travelled graphically.
Let t1 be the time of acceleration and t2 that of decelration of the bus.
The total time is t=t1+t2.
Let vmax be the maximum velocity.
As the acceleration and deceleration are constants the velocity time graph is a straight line as shown in the figure with +ve slope for acceleration and -ve slope for deceleration.From the graph,the slope of the line OA gives the acceleration α.
∴α =slope of the line OA=vmaxt1⇒t1=vmaxα
The slope of AB gives the deceleration β
∴β=slopeofAB=vmaxt2⇒t2=vmaxβ
t=t1+t2=vmaxα+vmaxβ
t=Vmax(α+βαβ)
∴vmax=(αβαβ)
∴vmax=(αβα+β)t
Displacement =area under the v-t graph ΔOAB
=12(base)(height)=12tvmax=12t(αβtα+β)=12(αβt2α+β)

Similar Questions
A bus accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds then, evaluate.
(a)the maximum velocity achieved and (b)the total distance travelled graphically.View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View Solution
Knowledge Check
- Question 1 - Select One
A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute the maximum velocity aquired by the car is
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate 'alpha' for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
View Solution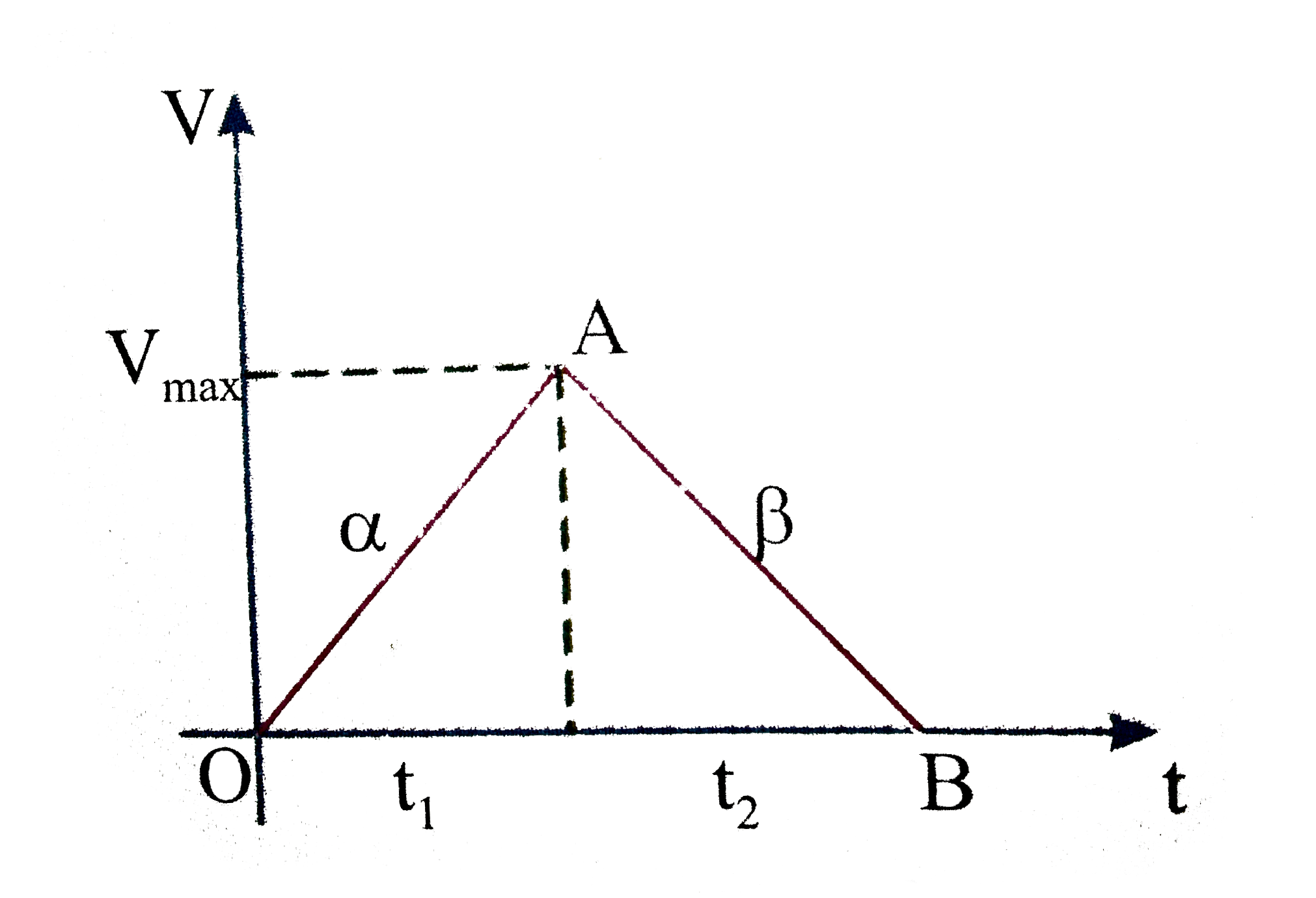
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.View Solution
