Refraction At Spherical Surfaces
Video Solution
Text Solution
The correct Answer is:NA
NA
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is
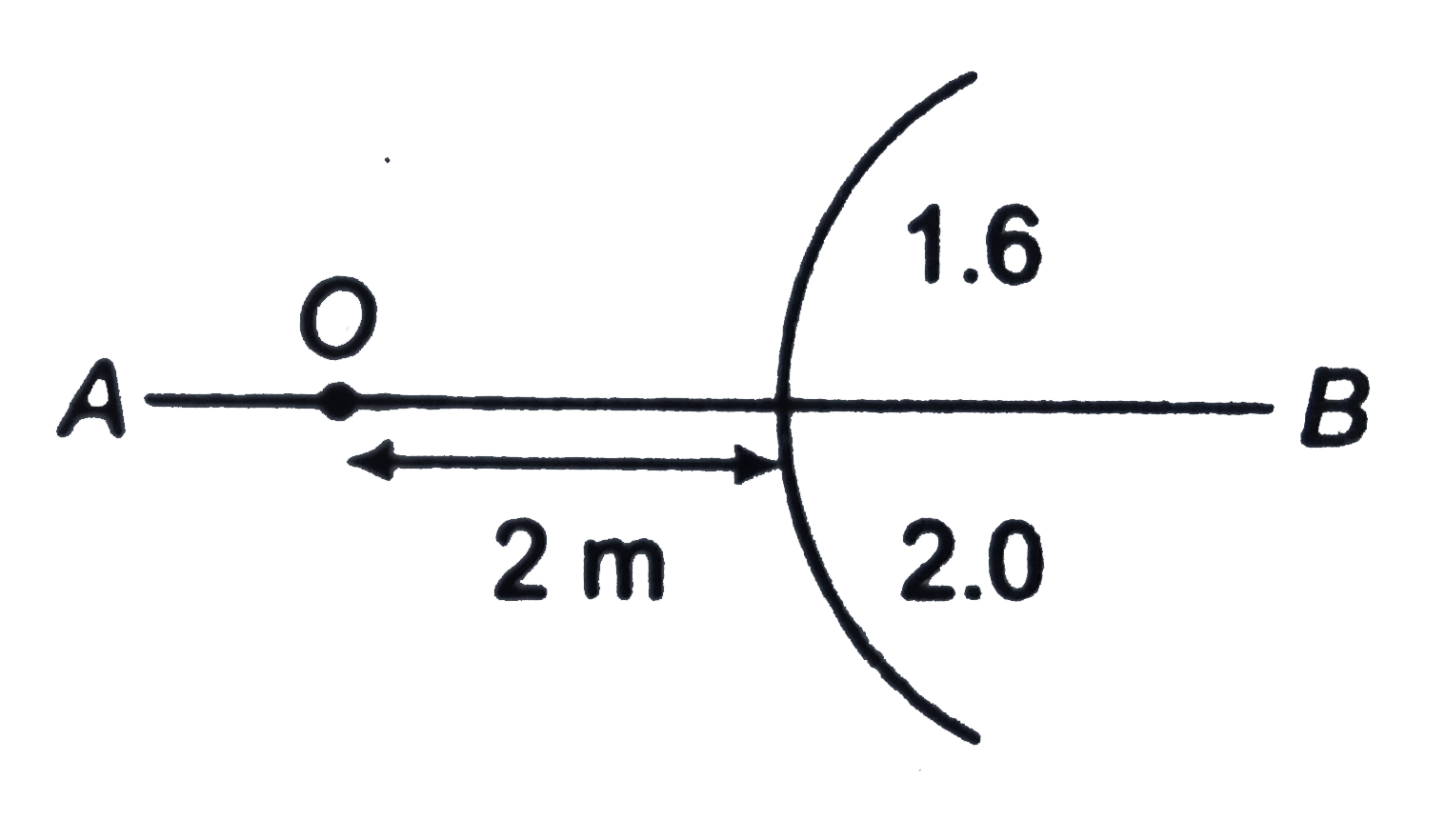 A12mB20mC14mD10m
A12mB20mC14mD10m - Question 2 - Select One or More
The first factor length f1 for refraction at a spherical surface is defined as the value of u corresponding to v=∞ (as shown) with refractive indices of two mediums, as n1 and n2. The second focal length f2 is defined as value of v for u=∞.
 Af2 is equal to n2R(n2−n1)Bf1 is equal to n2R(n2−n1)Cf2 is equal to (-) n2R(n2−n1)Df1 is equal to (-) n2R(n2−n1)
Af2 is equal to n2R(n2−n1)Bf1 is equal to n2R(n2−n1)Cf2 is equal to (-) n2R(n2−n1)Df1 is equal to (-) n2R(n2−n1) - Question 3 - Select One
A parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
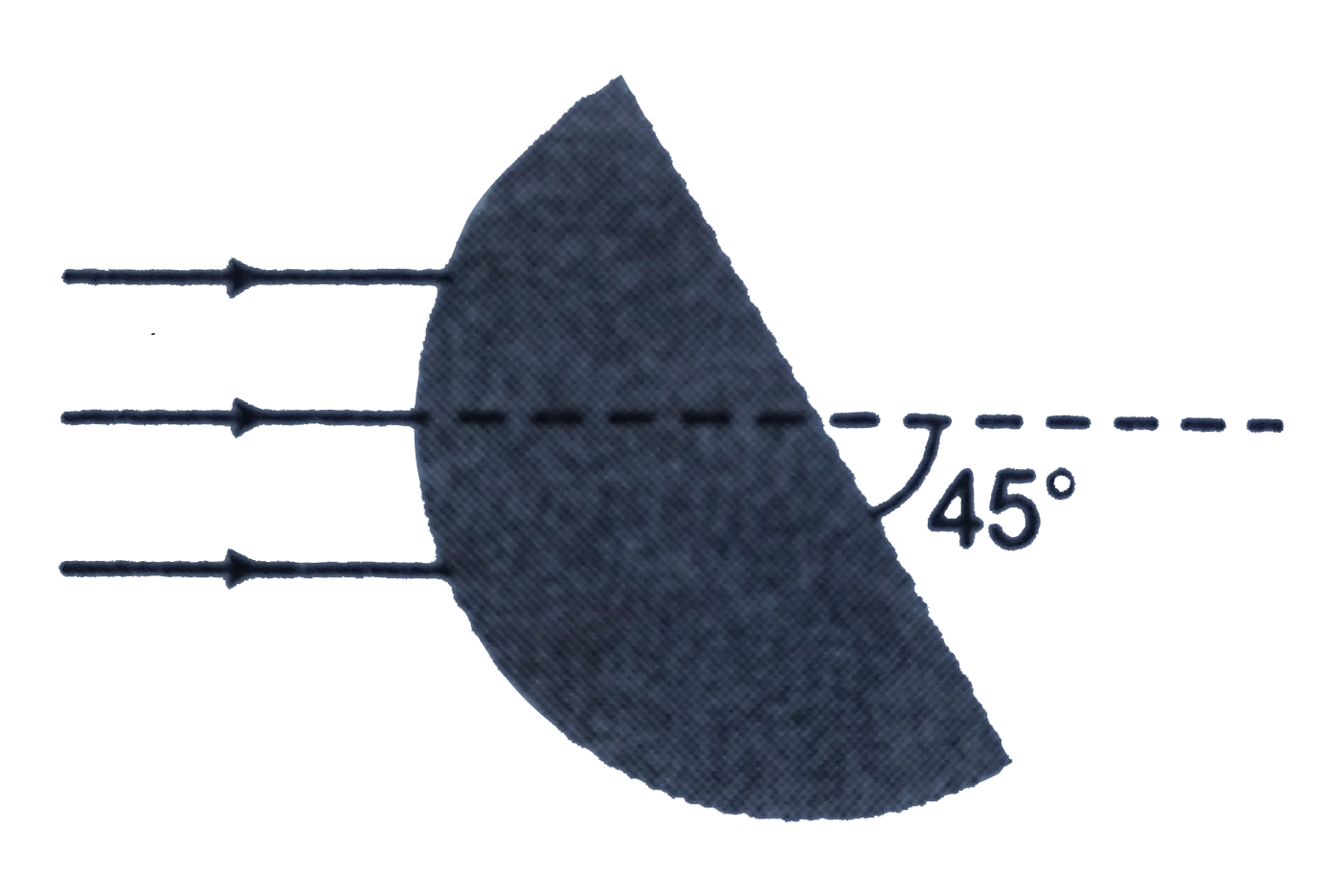 AR2B3RCR3D2R
AR2B3RCR3D2R
Refraction Concept||Plane Surface Refraction||Spherical Surface Refraction||Lateral Shift OF Ray by Slab
View SolutionThe equation of refraction at a spherical surface is μ2v−μ1u=μ2−μ1R
Taking R=∞, show that this equation leads to the equation
RealdepthApparentdepth=μ2μ1 for fraction at a plane surface.View SolutionRefraction on curved spherical surface||Examples OF refraction spherical surface
View SolutionRefraction Of Light|The Refractive Index|Refraction BY Spherical Lenses
View SolutionAn object is placed 10cm away form a glass piecwe (n=1.5) of length 20cm bounded by spherical surfaces of radii of curvaure 10cm. Find the position of final image formed after two refractions at the spherical surfaces.
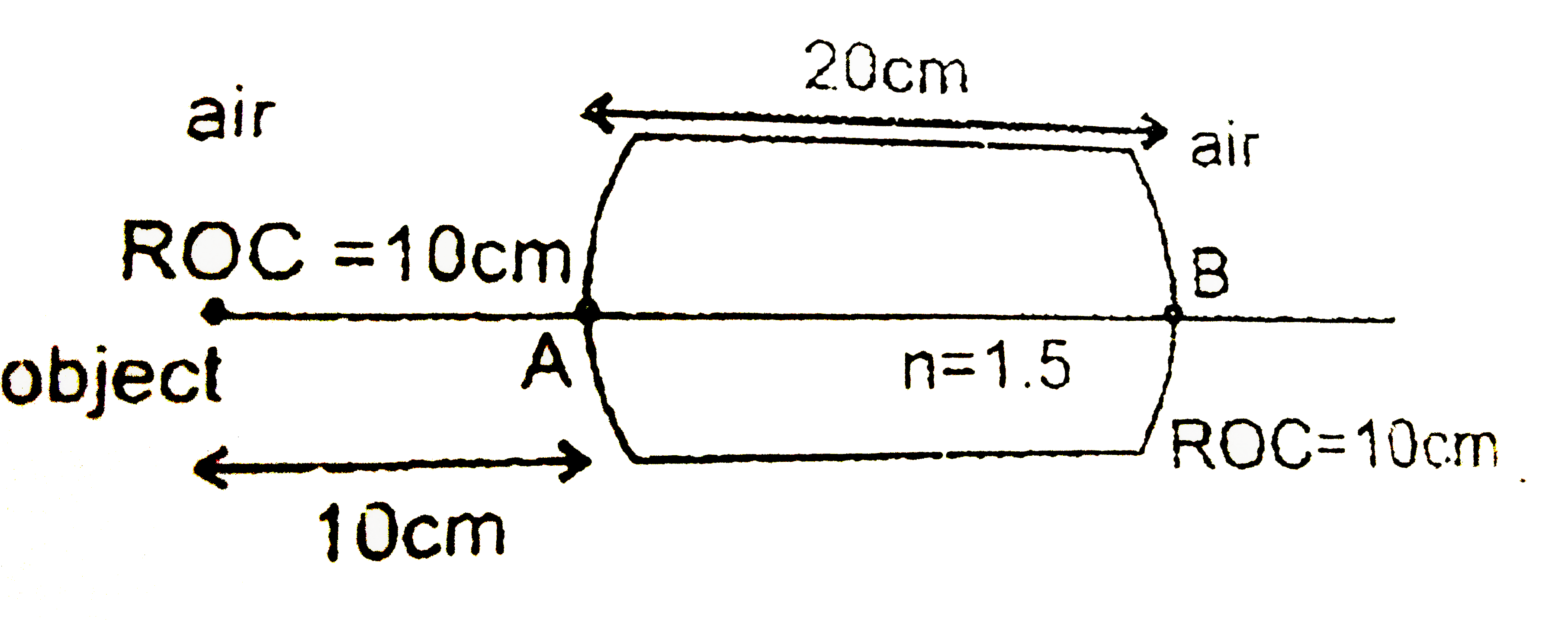 View Solution
View Solution

