Question

A particle of mass m and charge q has an initial velocity $\overrightarrow{v}=v_0\hat{j}$. If an electric field $E=E_0\hat{i}$ and $B=B_0\hat{i}$ magnetic field act on the particle, its speed will double after a time

Options

A. `t=(sqrt(3)mv_(0))/(qE)`
B. `t=(sqrt(2)mv_(0))/(qE)`
C. `t=(mv_(0))/(qE)`
D. `t=(mv_(0))/(2qE)`

Answer

A

Explanation

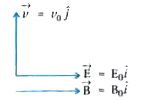
Magnitude of velocity doesn.t change in Y-Z plane.
`(2v_(0))^(2) =v_(0)^(2) +v_(x)^(2)`
`therefore v_(x) = sqrt(3)v_(0)`
`therefore` From equation of motion,
`v_(x) =v_(0x) + a_(0x)t`
`therefore sqrt(3)v_(0) =(qE)/mt, therefore t=(sqrt(3)mv_(0))/(qE)`