A body moving in a straight line with uniform acceleration describes three successive equal distances in time intervals t1,t2andt3 respectively. Show that
1t1−1t2+1t3=3t1+t2+t3
To solve the problem, we need to show that:
1t1−1t2+1t3=3t1+t2+t3
Given that a body moving with uniform acceleration covers three successive equal distances in time intervals t1, t2, and t3, we can denote the equal distance covered as x.
Step 1: Express average velocities for each segment
For each segment of the motion, we can express the average velocity as follows:
1. For the distance x covered in time t1:
v_{avg1} = \frac{x}{t_1} = \frac{v_1 + v_2}{2} \quad \text{(where v_1istheinitialvelocityandv_2 is the final velocity)}
Rearranging gives:
1t1=v1+v22x(Equation 1)
2. For the distance x covered in time t2:
vavg2=xt2=v2+v32
Rearranging gives:
1t2=v2+v32x(Equation 2)
3. For the distance x covered in time t3:
vavg3=xt3=v3+v42
Rearranging gives:
1t3=v3+v42x(Equation 3)
Step 2: Substitute and simplify
Now we substitute the expressions for 1t1, 1t2, and 1t3 into the equation we need to prove:
1t1−1t2+1t3=v1+v22x−v2+v32x+v3+v42x
Combining these fractions gives:
=(v1+v2)−(v2+v3)+(v3+v4)2x
Step 3: Cancel terms
Notice that v2 and v3 cancel out:
=v1+v42x
Step 4: Average velocity for the total distance
Now, consider the total distance covered, which is 3x in total time t1+t2+t3:
vavg=3xt1+t2+t3=v1+v42
Thus, we can express v1+v4 as:
v1+v4=3xt1+t2+t3⋅2
Step 5: Substitute back
Substituting this back into our equation gives:
1t1−1t2+1t3=3x(t1+t2+t3)⋅2x=3t1+t2+t3
Conclusion
Thus, we have shown that:
1t1−1t2+1t3=3t1+t2+t3
For each segment of the motion, we can express the average velocity as follows:
v_{avg1} = \frac{x}{t_1} = \frac{v_1 + v_2}{2} \quad \text{(where v_1istheinitialvelocityandv_2 is the final velocity)}
1t1=v1+v22x(Equation 1)
vavg2=xt2=v2+v32
1t2=v2+v32x(Equation 2)
vavg3=xt3=v3+v42
1t3=v3+v42x(Equation 3)
Now we substitute the expressions for 1t1, 1t2, and 1t3 into the equation we need to prove:
=(v1+v2)−(v2+v3)+(v3+v4)2x
Notice that v2 and v3 cancel out:
=v1+v42x
Now, consider the total distance covered, which is 3x in total time t1+t2+t3:
vavg=3xt1+t2+t3=v1+v42
v1+v4=3xt1+t2+t3⋅2
Substituting this back into our equation gives:
1t1−1t2+1t3=3x(t1+t2+t3)⋅2x=3t1+t2+t3
Thus, we have shown that:
1t1−1t2+1t3=3t1+t2+t3
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (DISTANCE AND DISPLACEMENT)
2 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (SPEED AND VELOCITY)
9 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
A point moving in a straight line with uniform acceleration describes aand b feet in successive intervals of t1 and t2 seconds. Then the acceleration is 2(bt1−at2)t1t2(t1+t2)
Also if the point describes equal distances in successive times t1,t2,t3 then
1t1−1t2+1t3=3t1+t2+t3
View SolutionA particle moves in a straight line with uniform acceleration and its distances from an origin O on the line (not necessarily the position at time t = 0) at times t1,t2,t3 are d1,d2,d3 respectively. Prove that if t1,t2,t3 form an A.P. whose common difference isd and d1,d2,d3 are in G.P. then the acceleration is(√d1−√d3)2d2
View Solution
Knowledge Check
A body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
Aa[t2+t1]2Ba[t2−t1]2Ct2∫t1a dtt2+t1Dt2∫t1a dtt2−t1A point moves with uniform acceleration and v1,v2 and v3 denote the average velocities in the three successive intervals of time t1,t2,andt3. Which of the following relations is correct
A(v1−v2):(v2−v3)=(t1−t2):(t2−t3)B(v1−v2):(v2−v3)=(t1+t2):(t2+t3)C(v1−v2):(v2−v3)=(t1−t2):(t1−t3)D(v1−v2):(v2−v3)=(t1−t2):(t2−t3)A point moves with uniform acceleration and v1,v2, and v3 denote the average velocities in the three successive intervals of time t1.t2, and t3 Which of the following Relations is correct?.
A(v1−v2):(v2−v3=(t1−t2:(t2+t3.B(v1−v2):(v2−v3=(t2−t2:(t2+t3C(v1−v2):(v2−v3=(t1−t2:(t2+t3D(v1−v2):(v2−v3=(t1−t2:(t2+t3
A body travels along a straight line with uniform acceleration a1 for time t1 and with uniform acceleration a2 for time t2 for time t2. What is the average acceleration?
View SolutionA point moves with uniform acceleration and v1,v2,v3 denote the average velocities in the successive intervals of times v1,v2,v3 . Then v1−v2v2−v3=t1+t2t2+t3
View SolutionTwo planets move around the sun. The periodic times and the mean radii of the orbits are T1,T2 and r1r2 respectively. The ratio T1/T2 is equal to
View SolutionA body is released from rest at t0=0,x0=0 and moves with constant acceleration. Its position is measured at the equally spaced times t1=Δt,t2=2Δt,t3=3Δt and so forth. Prove that displacements Δxj−xj−1 which occur in the successive time intervals Δt are in the ratio
Δx1:Δx2:Δx3......≈1:3:5...
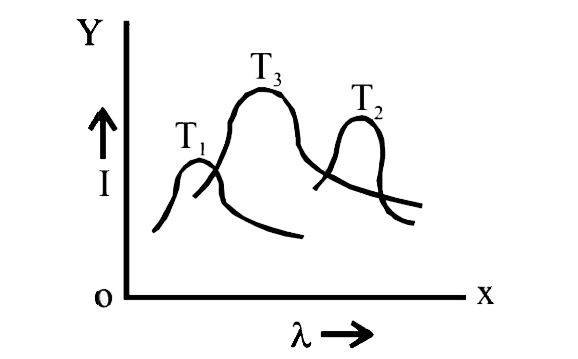
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
View Solution
