A train starts from rest and for the first kilometer moveswith constant acceleration. For the next 3 kilometers it has constant velocity and for another two kilometers it moves with constant retardation to come to rest after a total time of 10 minutes. The maximum velocity of the train is
18 km/h
36 km/h
54 km/h
39 km/h
The correct Answer is:C
To find the maximum velocity of the train, we can break down the problem into three segments based on the train's motion: acceleration, constant velocity, and retardation.
1. Identify the segments of motion:
- Segment 1: Acceleration over the first 1 km.
- Segment 2: Constant velocity over the next 3 km.
- Segment 3: Retardation over the last 2 km.
2. Define variables:
- Let v be the maximum velocity reached after the first segment.
- Let t1 be the time taken to travel the first 1 km.
- Let t2 be the time taken to travel the next 3 km at constant velocity v.
- Let t3 be the time taken to travel the last 2 km while decelerating to rest.
3. Equations for each segment:
- For Segment 1 (acceleration):
s1=12at21=1 km
Here, s1 is the distance (1 km), and a is the acceleration.
- For Segment 2 (constant velocity):
s2=vt2=3 km
- For Segment 3 (retardation):
s3=vt3−12at23=2 km
Here, a is the deceleration.
4. Total time:
The total time for the journey is given as 10 minutes, which we convert to hours:
ttotal=10 minutes=1060 hours=16 hours
Therefore:
t1+t2+t3=16 hours
5. Relate distances and times:
From the equations for the distances:
- From Segment 1, we can express t1 in terms of v:
v=at1(from v=u+at, where u=0)
Using s1=1 km:
1=12at21⟹a=2t21
Substitute a into the equation for v:
v=2t21t1=2t1
6. Substituting into total time:
Now we can express t2 and t3 in terms of v:
- From Segment 2:
t2=3v
- From Segment 3:
Using s3=2 km:
2=vt3−12at23
Substitute a:
2=vt3−12(2t21)t23
Rearranging gives:
2=vt3−t23t21
7. Combine equations:
Substitute t1,t2,t3 into the total time equation:
t1+3v+t3=16
8. Solve for v:
After substituting and simplifying, we find that:
v=54 km/h
Final Answer:
The maximum velocity of the train is 54 km/h.
- Segment 1: Acceleration over the first 1 km.
- Segment 2: Constant velocity over the next 3 km.
- Segment 3: Retardation over the last 2 km.
- Let v be the maximum velocity reached after the first segment.
- Let t1 be the time taken to travel the first 1 km.
- Let t2 be the time taken to travel the next 3 km at constant velocity v.
- Let t3 be the time taken to travel the last 2 km while decelerating to rest.
- For Segment 1 (acceleration):
s1=12at21=1 km
Here, s1 is the distance (1 km), and a is the acceleration.
- For Segment 2 (constant velocity):
s2=vt2=3 km
- For Segment 3 (retardation):
s3=vt3−12at23=2 km
Here, a is the deceleration.
The total time for the journey is given as 10 minutes, which we convert to hours:
ttotal=10 minutes=1060 hours=16 hours
Therefore:
t1+t2+t3=16 hours
From the equations for the distances:
- From Segment 1, we can express t1 in terms of v:
v=at1(from v=u+at, where u=0)
Using s1=1 km:
1=12at21⟹a=2t21
Substitute a into the equation for v:
v=2t21t1=2t1
Now we can express t2 and t3 in terms of v:
- From Segment 2:
t2=3v
- From Segment 3:
Using s3=2 km:
2=vt3−12at23
Substitute a:
2=vt3−12(2t21)t23
Rearranging gives:
2=vt3−t23t21
Substitute t1,t2,t3 into the total time equation:
t1+3v+t3=16
After substituting and simplifying, we find that:
v=54 km/h
The maximum velocity of the train is 54 km/h.
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (RELATIVE VELOCITY)15videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (VECTORS)23videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (GRAPHICAL STUDY OF MOTION)16videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS32videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)24videos
LAWS OF MOTION
Similar Questions
A car starts from rest and moves along the x-axis with constant acceleration 5ms−2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest ?
View SolutionA train starts from a station and moves with a constant acceleration for 2 minutes. If it covers a distance of 400m in this period, find the acceleration.
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A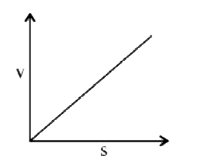 B
B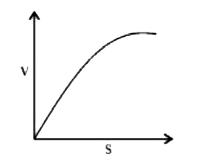 C
C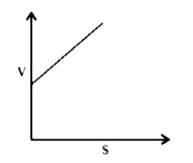 D
D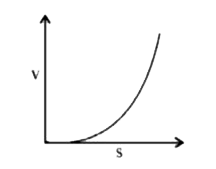
- Question 2 - Select One
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b) - Question 3 - Select One
A train starting from rest travels the first part of its journey with constant acceleration a, secondpart with constant velocity v nd third part with constant retardation a, being brought to rest.the average speed for the whole journey is7v8. The train travels with constant velocity for...of the total time -
A34B78C56D97
A train starting from rest travels the first part of its journey with constant acceleration f1, the second part with constant speed v and the third part with constant retardation f2 and is then reduced to rest again. If the average speed for the whole journey be 78v then the train is travelling at constant speed for three-quarters of the total time and describes 6/7 of total distance.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
View SolutionA car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View Solution

