A vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
A
ˆi+ˆj
B
4ˆj
C
ˆj+ˆk
D
−7ˆk
Video Solution
Text Solution
The correct Answer is:D
The vector product of two non-zero vectors is zero of they are in the same direction or in the opposite direction. Hence vector →B must be parallel or antiparallel to vector →A. along ±z - axis
|
Updated on:21/07/2023
Related Playlists
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )23videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (PROJECTILE MOTION)58videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (VECTORS)23videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS32videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)24videos
LAWS OF MOTION
Similar Practice Problems
- Question 1 - Select One
A vector →A is along the positive x-axis and its vector product with another vector →B is zero, then vector →B could be
Aˆi+ˆjB4ˆiCˆj+ˆkD−7ˆk - Question 1 - Select One
A vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
A4jB−4iC−(i+j)D(j+k) - Question 1 - Select One
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .A120B90C60D150
.A120B90C60D150 - Question 1 - Select One
The magnitude of the vectors product of two vectors ∣∣→A∣∣and∣∣→B∣∣ may be
Agreater than ABBequal to ABCless than ABDequal to zero - Question 1 - Select One or More
Vector →A−→B represents -
AAddition of vector →A and vector −→B.BResultant of vector →Aand→BCResultant of vector →Aand−→BDNone of these - Question 1 - Select One
Resolved part of vector →a and along vector →b is →a1 and that prependicular to →b is →a2 then →a1×→a2 is equl to
A(→a×→b).→b∣∣→b∣∣2B(→a.→b)→a|→a|2C(→a.→b)(→b×→a)∣∣→b∣∣2D(→a.→b)(→b×→a)∣∣→b×→a∣∣
Similar Questions
A vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionA vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionThe magnitude of the vector product of two vectors →A and →B may not be:
View SolutionA vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
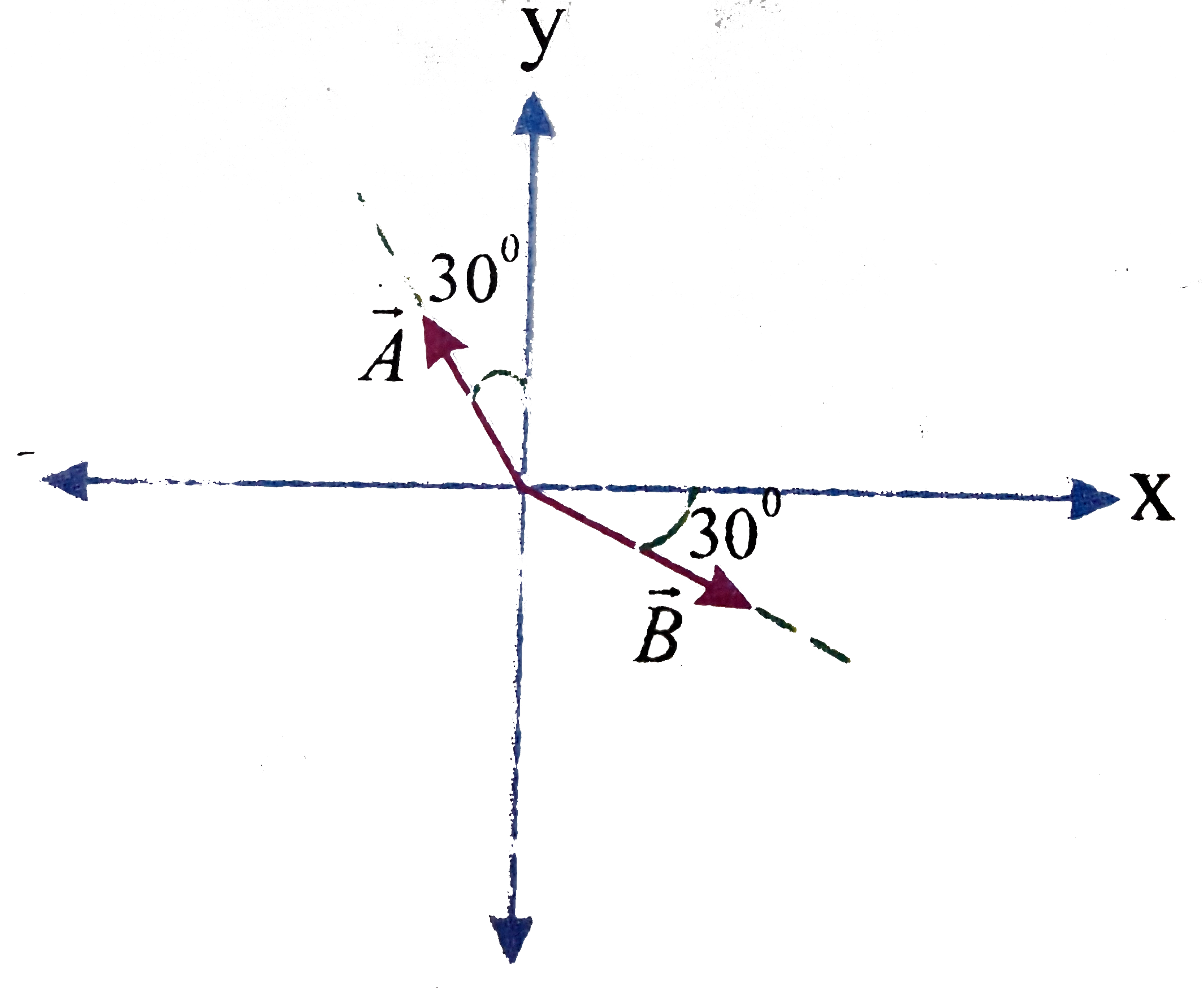 View Solution
View Solution

