A particle is moving on circular path as shown in the figure. Then displacement from P1 to P2 is

A
2rcos(θ)2
B
2rtan(θ)2
C
2rsinθ
D
2rsin(θ)2
Text Solution
The correct Answer is:D
According to cosine formula
cosθ=r2+r2−x22r2
or 2r2cosθ=r2+r2−x2
or x2=2r2−2r2cosθ=2r2[1−cosθ]=2r2[2sin2θ2]
Displacement from P1 to P2 is x=2rsin(θ)2

|
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (PROJECTILE MOTION)
58 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)
8 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (SCALAR AND VECTOR PRODUCTS OF VECTORS )
16 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
Knowledge Check
A particle is moving in a circular path of radius r. The displacement after half a circle would be
AzeroBπrC2rD2π rA particle is moving in a circular path of radius r. The displacement after half a circle would be
AzeroBπrC2rD2π rA particle is moving in a circular path of radius r. The displacement after half a circle would be
AzeroBπrC2rD2π r
A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle is moving in a circular path of radius 'r'. The displacement after half a circle would be
View SolutionA particle travels from A to B path shown in figure, then the displacement of particle is :
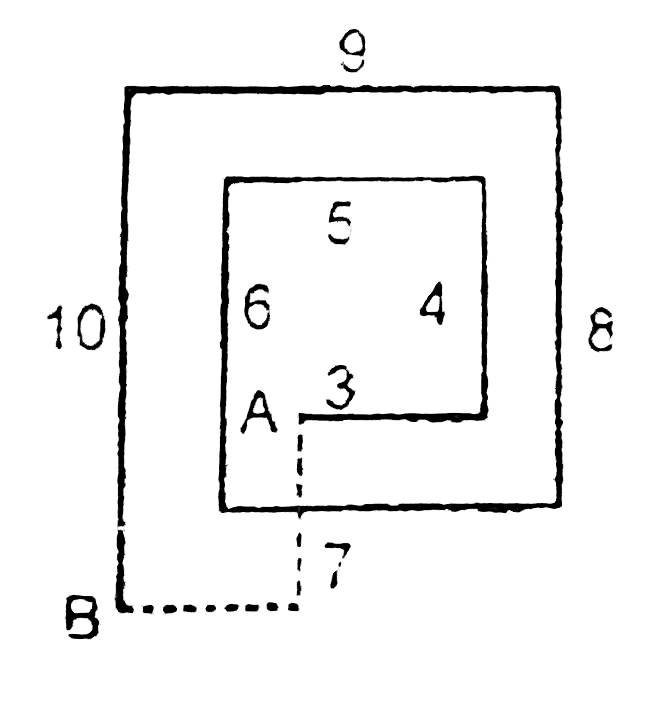 .
.
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is

View Solution
