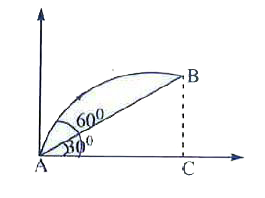
Time taken by the projectile to reach from A to B ist, then the distance AB is equal to

2ut
√3 ut
√32 ut
ut√3
The correct Answer is:D

From figure Horizontal components of velocity at A is
uH=ucos60∘=u2∴AC=uH×t=ut2
AB=ACsec30∘=ut2×2√3=ut√3
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)
8 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )
23 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
Knowledge Check
In the time taken by the projectile to reach from A to B is t. Then the distance AB is equal to.
 .Aut√3B√3ut2C√3utD2ut
.Aut√3B√3ut2C√3utD2utTime taken by the particle to reach from A to B is t. Then the distance AB is equal to
 Aut√3B√3ut2C√3utD2ut
Aut√3B√3ut2C√3utD2utIf time taken by the projectile to reach Q is T, than PQ=
 ATvsinθBTvcosθCTvsecθDTvtanθ
ATvsinθBTvcosθCTvsecθDTvtanθ
If time taken by the projectile to reach B is T, then AB is equal to

View SolutionIf time taken by the projectile to reach Q is T, than PQ=

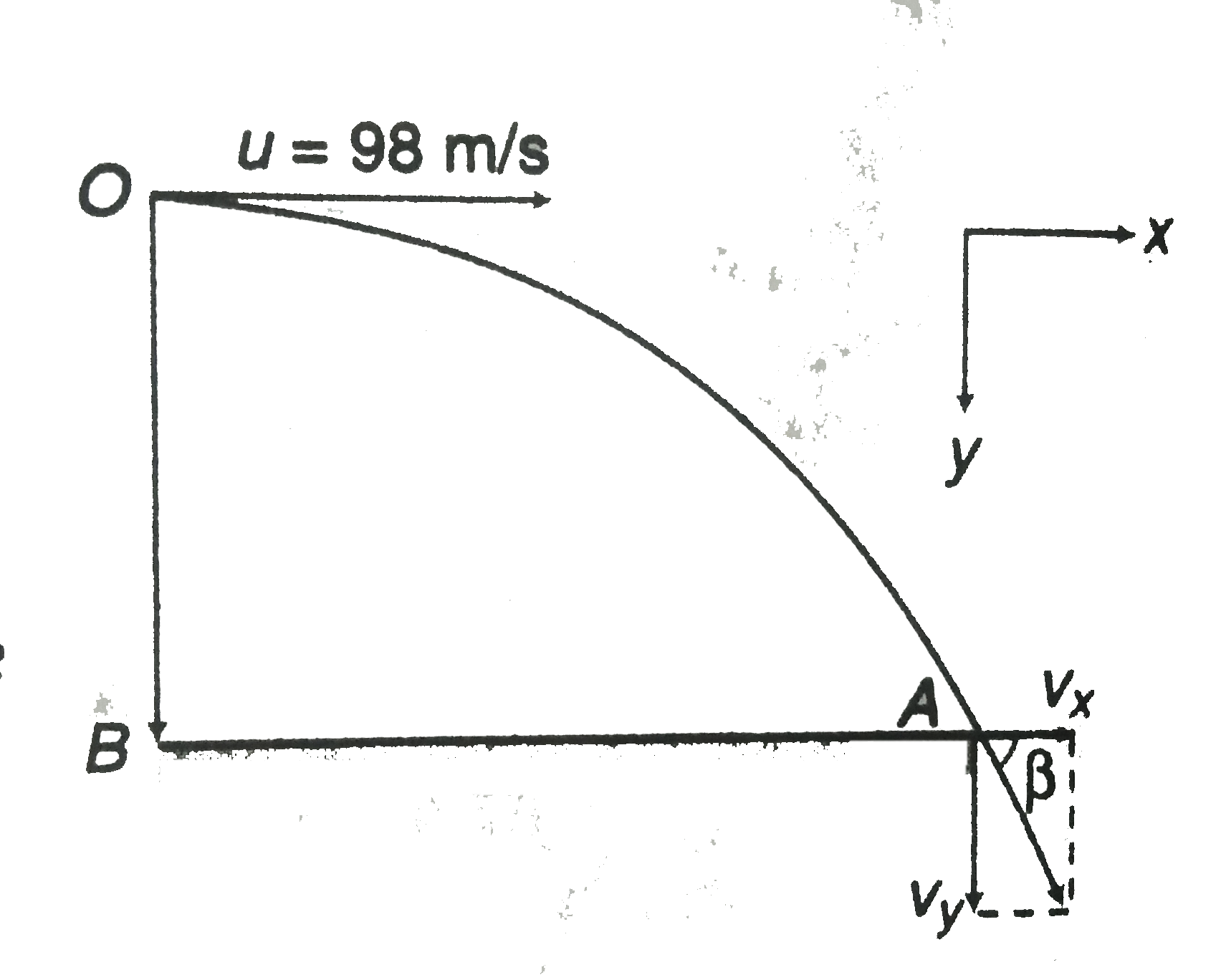
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
View SolutionFrom the top of a hill 480 m high , a projectile is fired horizontally with a speed of 96m/s . Calculate
(i) the time taken by projectile to reach the ground .
(ii) the distance of the target from the hill .
(iii) the velocity with which the projectile hits the ground . Take g=10ms−2
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
View Solution