If vectors →A=cosωtˆi+sinωtˆj and →B=cos(ωt2)ˆi+sin(ωt2)ˆj are functions of time then the value of t at which they are orthogonal to each other is (A) t=πw (B) t=0 (C) t=π4w (D) t=π2w
t=πω
t = 0
t=π4ω
t=π2ω
Step by step video & image solution for If vectors vec A= cos omega t hat i + sin omega t hat j and vecB= cos ((omega t)/2) hat i +sin ((omega t)/(2)) hat j are functions of time then the value of t at which they are orthogonal to each other is (A) t=pi/w (B) t=0 (C) t=pi/(4w) (D) t=pi/(2w) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If Vectors →A=cosωˆi+sinωˆj and →B=(cos)ωt2ˆi+(sin)ωt2ˆjare functions of time. Then the value of t at which they are orthogonal to each other is
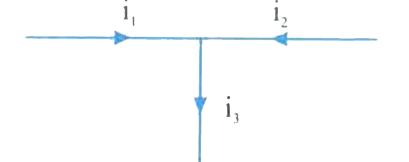
At=0Bt=π4ωCt=π2ωDt=πωIf i1=3sinωtand(i2)=4cosωt, then (i3) is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)A particle moves so that its position vector is given by →r=cosωtˆx+sinωtˆy, where ω is a constant which of the following is true ?
AVelocity is perpendicular to →r and acceleration is directed away from the origin.BVelocity and acceleration both are perpendicular to →r.CVelocity and acceleration both are parallel to →r.DVelocity is perpendicular to →r and acceleration is directed towards the origin.
In y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
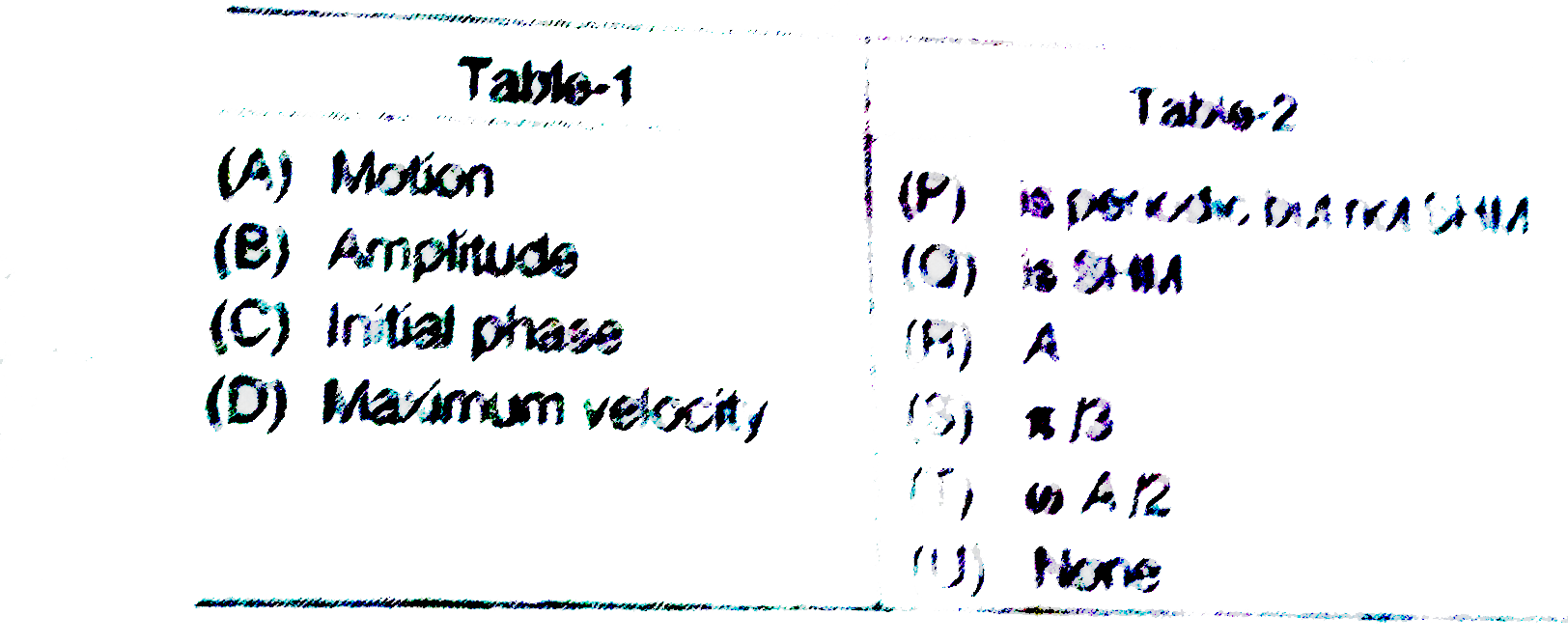
View SolutionFind time period of the function, y=sinωt+sin2ωt+sin3ωt
View SolutionEquations y=2Acos2ωtandy=A(sinωt+√3cosωt) represent the motion of two particles.
View SolutionThe position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle is
View SolutionPosition vector of a particle moving in x−y plane at time t is r=a(1−cosωt)ˆi+asinωtˆj. The path of the particle is
View Solution