A large open tank has two holes in its wall. Ine is a square hole of side a at a depath of x from the top and the other is a cirular hle of radius r at a depth 4x from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then r is equal to
2πa
a2π
aπ
a√2π
The correct Answer is:D
Speed of the water coming out from the hole, v=√2gh
where h denotes depth of the hole from the free surface of the water in the tank. The quantities of water flowing out per second from both holes are given to be same, therefore A1v1=A2v2
where A1andA2 are the area of cross-sections of hole 1 (i.e. square hole) and hole 2 (i.e, circular hole) and v1andv2 are speed of water coming out from these holes.
∴a2√2gx=πr2√2g4xora2=2πr2
or r2=a22πorr=a√2π
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals22videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ14videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)26videos
THERMODYNAMICS
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth h from the top and the other is a circular hole of radius r at a depth 4h from the top. Whwn the tank is completely filled with water, the quantity of water flowing out per second from both the holes are the same. What is the value of r?
View SolutionA vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
View Solution
Knowledge Check
- Question 1 - Select One
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
A(a) L√2πB(b) 2πLC(c) LD(d) L2π - Question 2 - Select One
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
AL√2πB2πLCL√2πDL2π - Question 3 - Select One
A large open tank has two holes in the wall. The top hole is a square hole of side L at a depth y from the surface of water. The bottom hole is a circular hole of radius R at a depth 4y from surface of water . If R=L/2√π, find the correct graph. V1 and V2 are the velocities in top and bottom holes. Area of the square & curcular holes are a1 and a2
A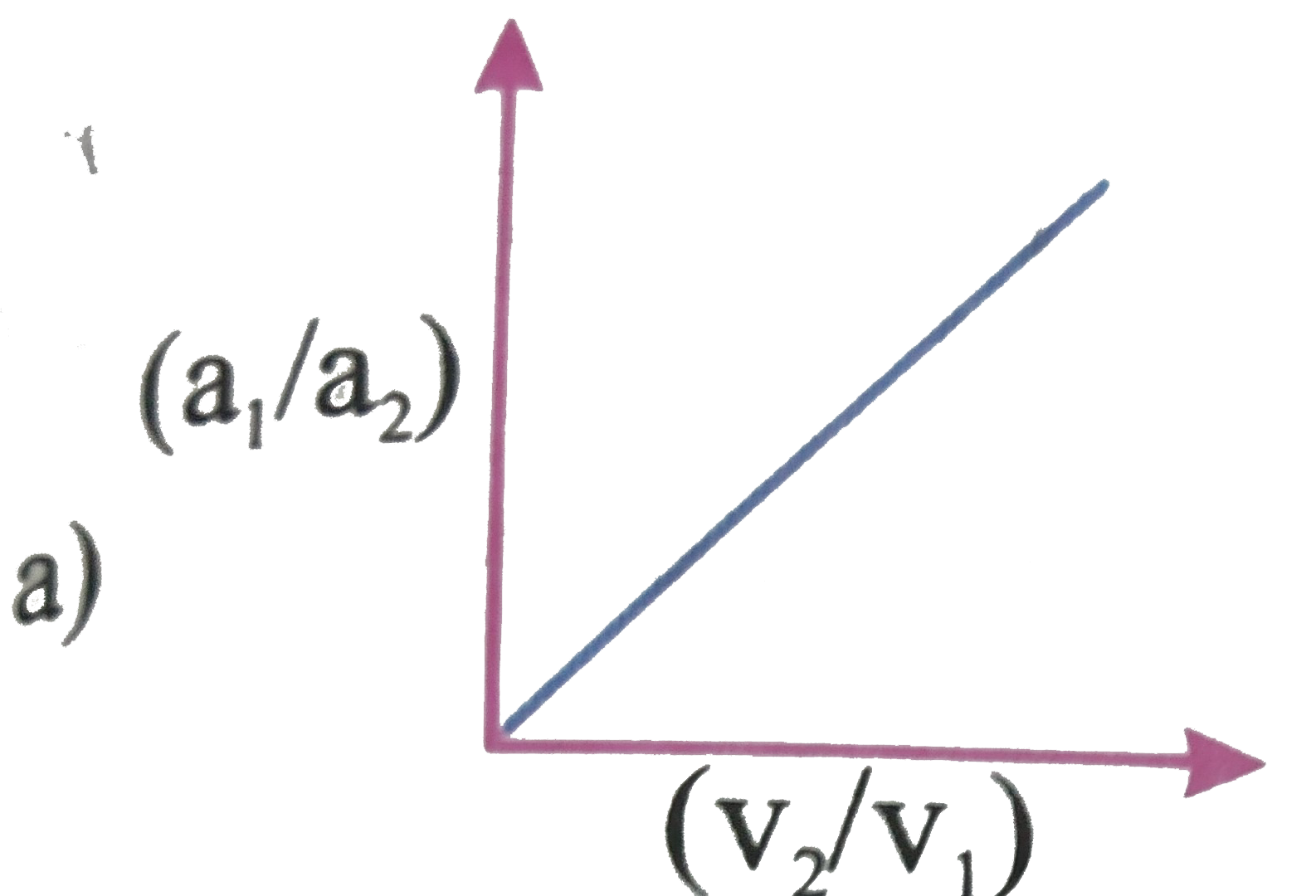 B
B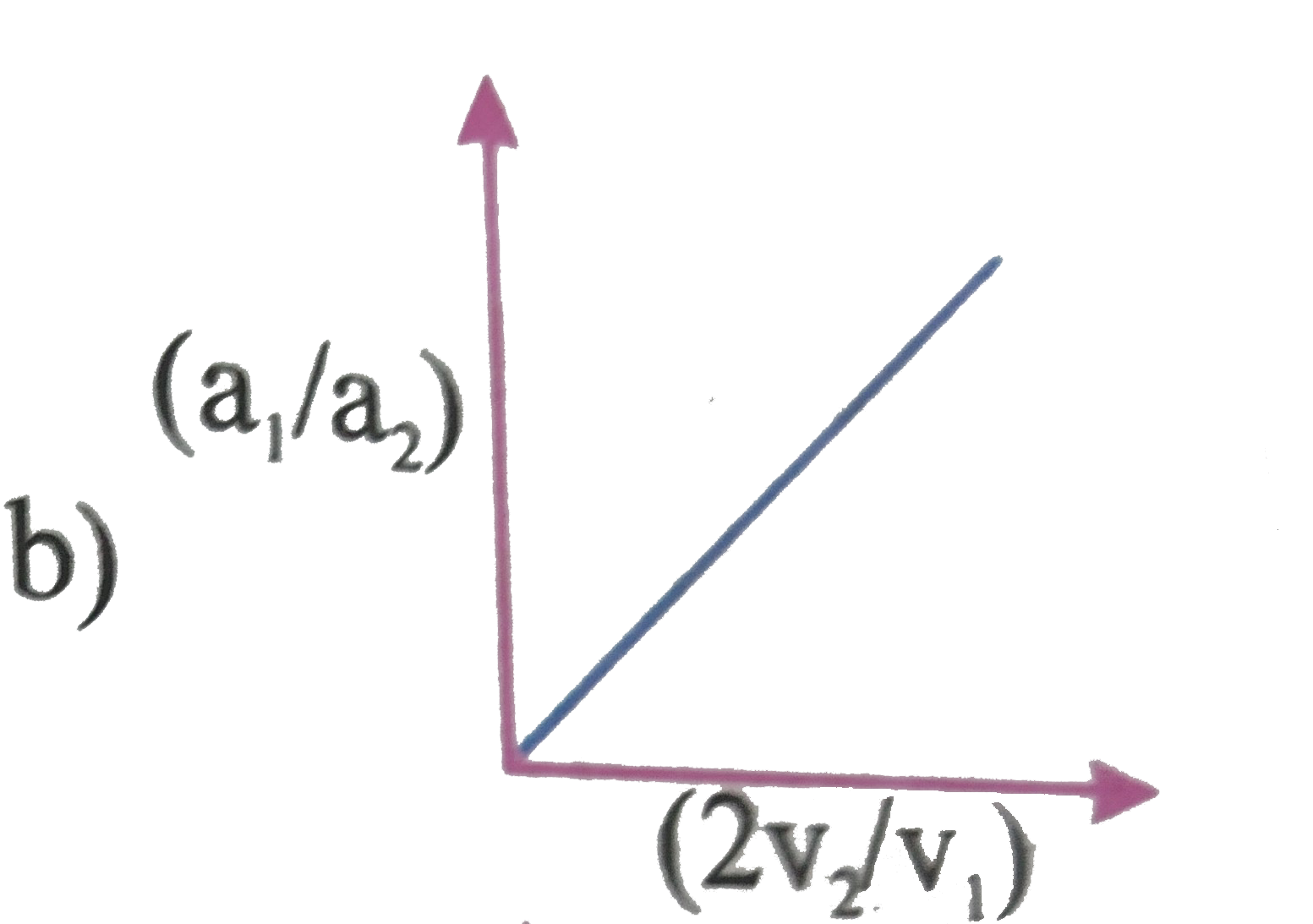 C
C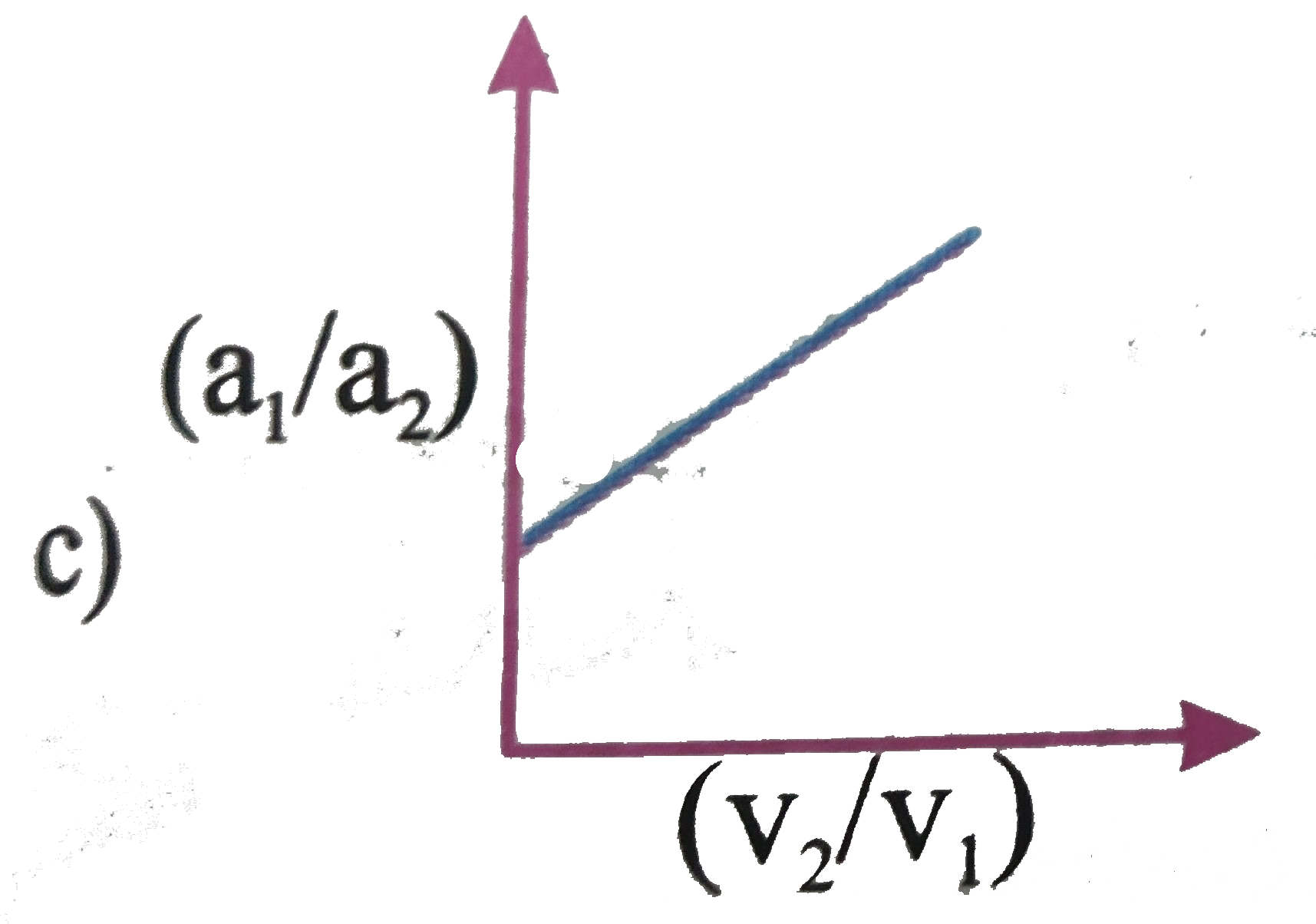 D
D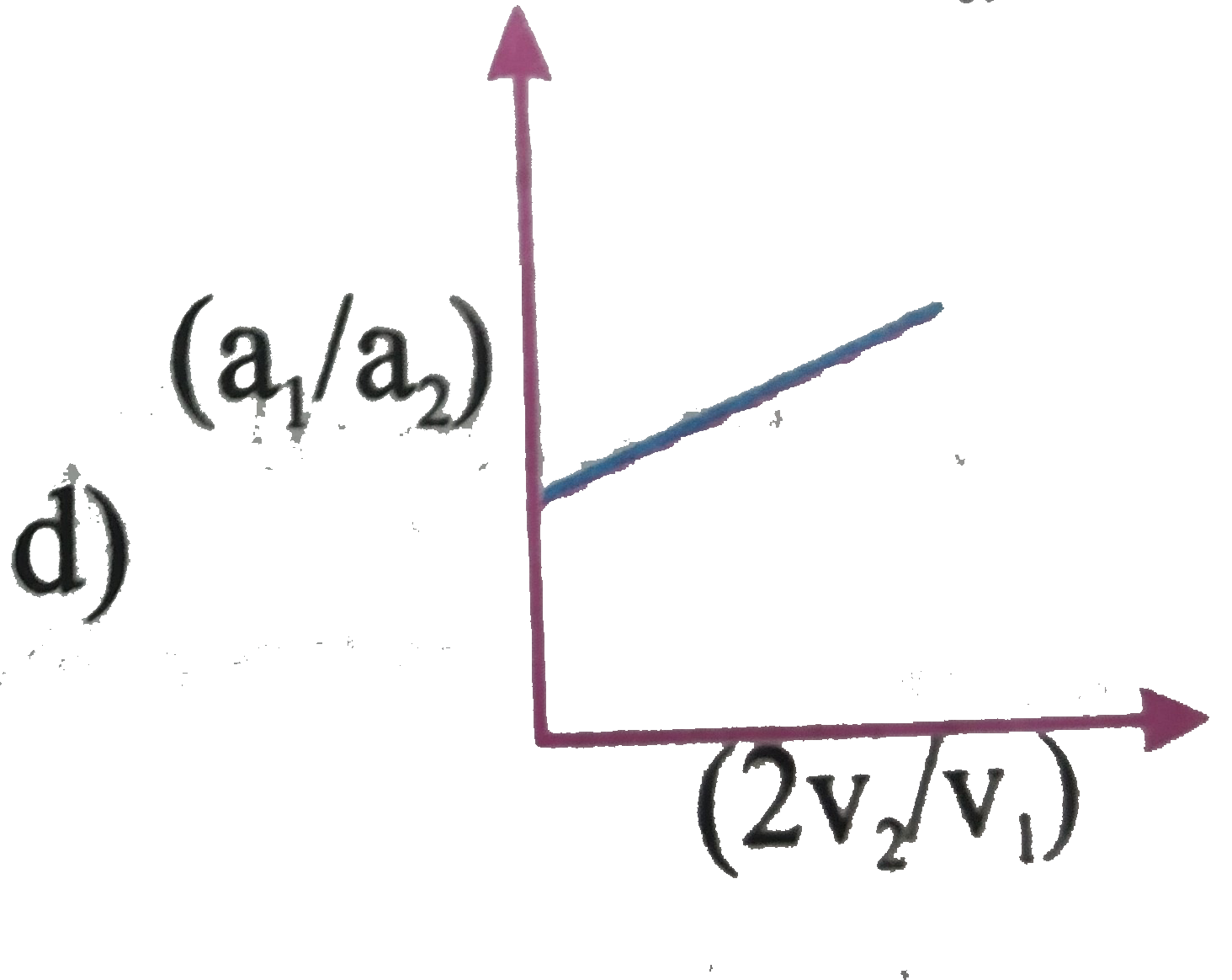
A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
View SolutionThere are two holes P and Q at depths h and 4h from the top of a large vessel, completely filled with water. P is a square hole of side L and Q is a circular hole of radius r. If the same quantity of water flows out per second from both the holes, then the relation between L and r is
View SolutionA vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '2h' from the top, respectivel. Hole 'A' is a square of side 'L' and 'B' is circle of radish 'r' The water flowing out per second from both the holes is same Then, 'L'is equal to
View SolutionThere is a hole h metre from its top of a tank filled with water. Calculate the distance x where the stream of water will touch the ground from the bottom (in m).
 View Solution
View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View Solution

