If O=(0,0),A=(1,0) and B=(12,√32) then centre of circle for which the lines OA, OB and AB are tangents is Solution in Telugu
(12),12√3
(12),(1√3)
(1√3,12)
(12√3,12)
The correct Answer is:A
Step by step video, text & image solution for If O=(0,0),A=(1,0) and B=(1/2,(sqrt(3))/2) then centre of circle for which the lines OA, OB and AB are tangents is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - PRACTICE EXERCISE
164 Videos
- CIRCLESBOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - EXERCISE -I
89 Videos
- CIRCLEBOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.4
38 Videos
- COMPLEX NUMBERSBOOK - AAKASH SERIESCHAPTER - COMPLEX NUMBERSEXERCISE - PRACTICE EXERCISE
93 Videos
Similar Questions
The circle with centre (1,1) and radius 1 is
View SolutionThe circle with centre (32,12) and radius √32 is
View SolutionDiscuss the relative position of the fol-
lowing pair of circles.
x2+y2−4x−6y−12=0
x2+y2+6x+18y+26=0.
View SolutionThe value of 13∑n=1(in+in+1) , where i=√−1 is
View SolutionConsider the circle: x^2+y^2=r^2 with centre O. A and B are collinear with O such that OA. OB=r^2. The number of circles passing through A and B, which are orthogonal to the circle C is
View SolutionO is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB=15cm . Find OB .
View SolutionTangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
View Solutionif P=(0,0),Q=(1,0) and R=((1)/(2),(sqrt(3))/(2)), then the centre of the circle for which the lines PO,QR and RP are tangents is
View SolutionIf A(0,0),B(1,0) and C((1)/(2),(sqrt(3))/(2)) then the centre of the circle for which the lines AB,BC,CA are tangents is
View SolutionA tangent AB, at a point A of a circle of radius 5 cm, meets a line through the centre O at point B such that OB =12 cm. Length AB is
View SolutionIf O=(0,0), A=(1,0) and B=(1/2,√3/2) then the centre of the circle for which the lines OA, Ab and BO are the tangents, is
View SolutionIf P(0,0,)Q(1,0)andR(12,√32) are three given points, then the centre of the circle for which the lines PQ,QR and RP are the tangents is
View Solutionयदि मूलबिंदु O से वृत्त x2+y2−6x−8y+21=0 पर खींची गई स्पर्श रेखाएं OA व OB हैं तब AB की लम्बाई है
View SolutionIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
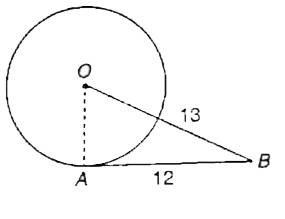
View SolutionA,B are conjugate points w.r.t circle having centre O radius r then OA2+OB2−2r2=AB2
View Solution
