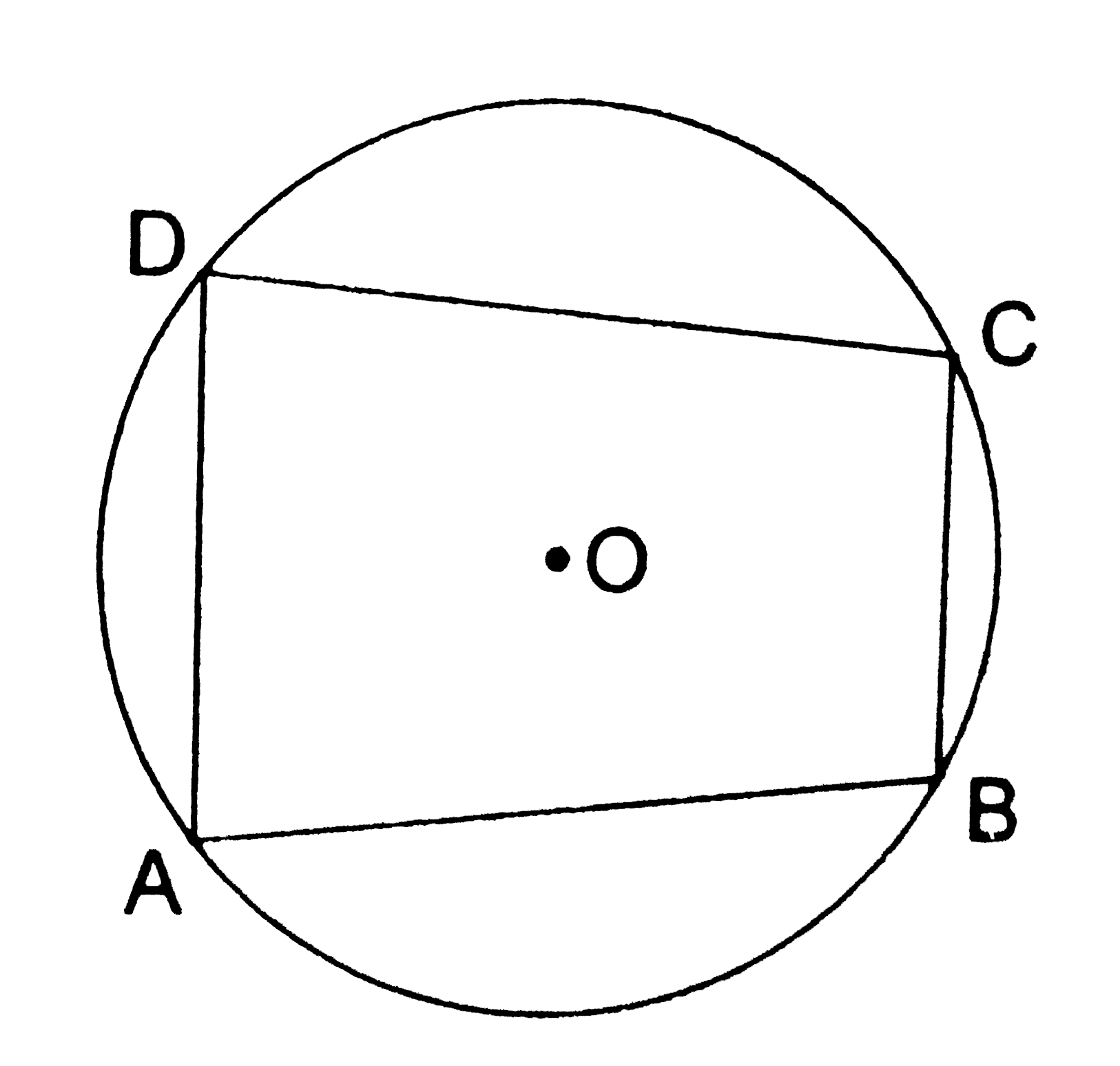
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Let ABCD be a cyclic quadrilateral and let O be the centre of the centre , passing through A,B,C,D. Then , each of AB, BC, CD and DA being a chord of the circle, its right bisector must pass through O .Hence, the right bisectors of AB, BC ,CD and DA pass through O .
Similar Questions
Show that the perpendicular bisectors of the sides of a triangle are concurrent.
View SolutionDefinition of Cyclic quadrilateral
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionThe opposite angles of a cyclic quadrilaterals are supplimentary
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is 180∘
View SolutionThe number of triangles that can be formed by the perpendiculars bisectors of the sides of a triangle is
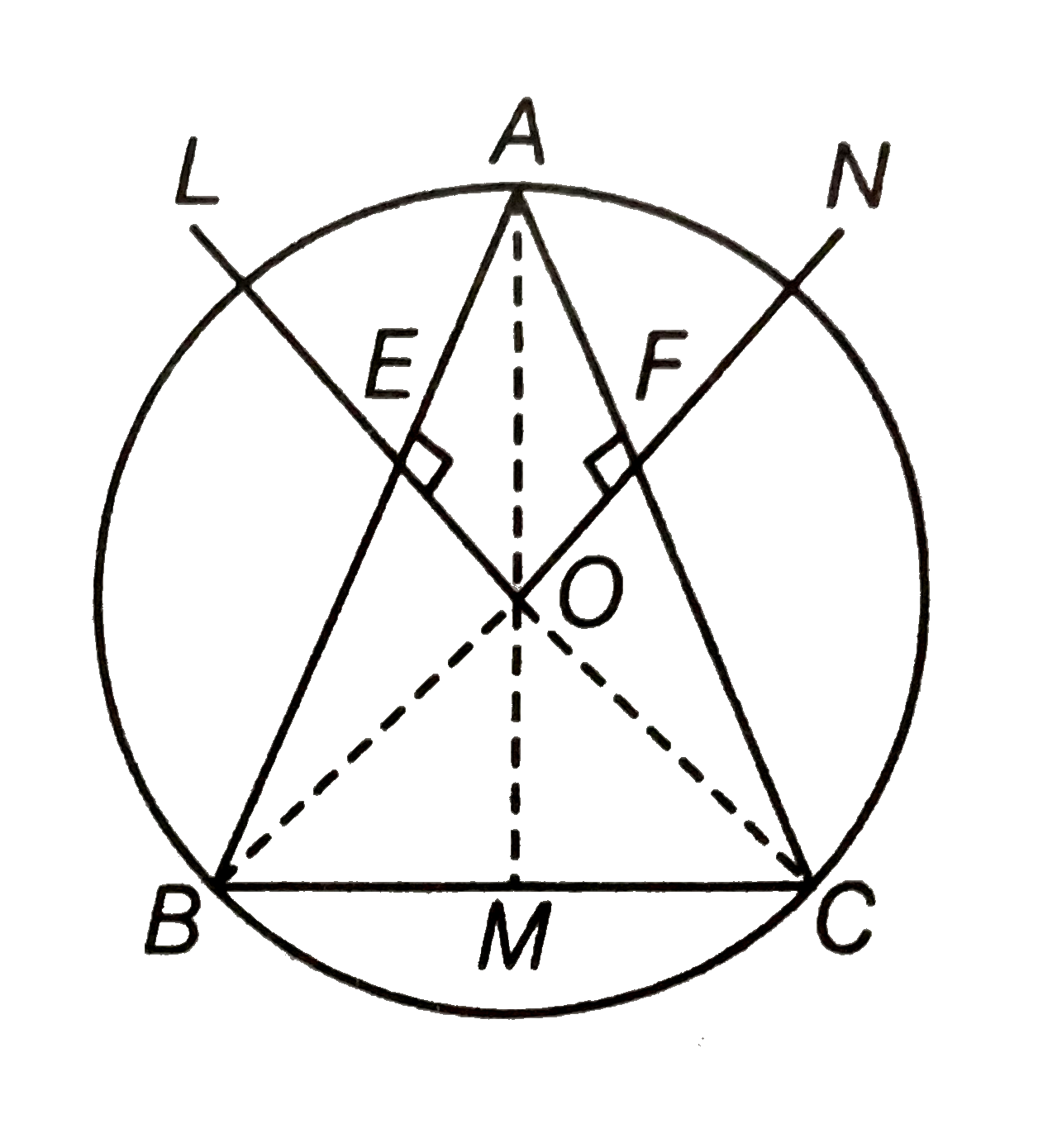
View SolutionA, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
 View Solution
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View Solution

