Two lines AB and CD intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all the four angles.
The correct Answer is:∠BOC=140∘,∠AOD=140∘,∠AOC=40∘,∠BOD=40∘
To solve the problem, we need to find the four angles formed by the intersection of lines AB and CD at point O, given that ∠BOC+∠AOD=280∘.
1. Identify the Angles:
Let ∠BOC=x and ∠AOD=y. According to the problem, we have:
x+y=280∘
2. Use the Property of Vertically Opposite Angles:
Since AB and CD intersect at point O, the angles ∠BOC and ∠AOD are vertically opposite angles. Therefore, we have:
x=y
3. Substitute and Solve:
Substitute y with x in the equation from step 1:
x+x=280∘
This simplifies to:
2x=280∘
Dividing both sides by 2 gives:
x=140∘
Thus, we find:
∠BOC=140∘and∠AOD=140∘
4. Find the Remaining Angles:
The other two angles ∠AOC and ∠BOD are also vertically opposite angles. Therefore:
∠AOC=∠BOD
Since ∠AOC+∠BOC=180∘ (as they are on a straight line), we can write:
∠AOC+140∘=180∘
Thus:
∠AOC=180∘−140∘=40∘
Therefore, we also have:
∠BOD=40∘
Summary of Angles:
- ∠BOC=140∘
- ∠AOD=140∘
- ∠AOC=40∘
- ∠BOD=40∘
Let ∠BOC=x and ∠AOD=y. According to the problem, we have:
x+y=280∘
Since AB and CD intersect at point O, the angles ∠BOC and ∠AOD are vertically opposite angles. Therefore, we have:
x=y
Substitute y with x in the equation from step 1:
x+x=280∘
This simplifies to:
2x=280∘
Dividing both sides by 2 gives:
x=140∘
Thus, we find:
∠BOC=140∘and∠AOD=140∘
The other two angles ∠AOC and ∠BOD are also vertically opposite angles. Therefore:
∠AOC=∠BOD
Since ∠AOC+∠BOC=180∘ (as they are on a straight line), we can write:
∠AOC+140∘=180∘
Thus:
∠AOC=180∘−140∘=40∘
Therefore, we also have:
∠BOD=40∘
- ∠BOC=140∘
- ∠AOD=140∘
- ∠AOC=40∘
- ∠BOD=40∘
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7C24videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Multiple Choice Questions (Mcq)28videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A12videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)24videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)18videos
MEAN , MEDIAN AND MODE OF UNGROUPED DATA
Similar Questions
Knowledge Check
- Question 1 - Select One
AB∣∣CD, shown in the figure. Find the value of x :
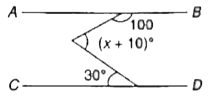 A100∘B90∘C110∘D140∘
A100∘B90∘C110∘D140∘ - Question 2 - Select One
Two lines AB and CD intersect at a point O.∠AOC=40∘,find the measure of each of the angles ∠AOD,∠BODand∠BOC.
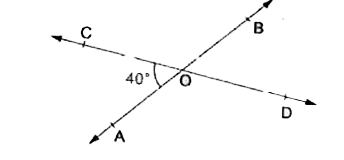 A∠AOD=160∘,∠BOD=40∘and∠BOC=160∘B∠AOD=110∘,∠BOD=40∘and∠BOC=110∘C∠AOD=140∘,∠BOD=40∘and∠BOC=140∘D∠AOD=150∘,∠BOD=50∘and∠BOC=140∘
A∠AOD=160∘,∠BOD=40∘and∠BOC=160∘B∠AOD=110∘,∠BOD=40∘and∠BOC=110∘C∠AOD=140∘,∠BOD=40∘and∠BOC=140∘D∠AOD=150∘,∠BOD=50∘and∠BOC=140∘
If two lines AB and CD intersect at O such that ∠AOC=5∠AOD, then the four angles at O are
View SolutionIn the given figure, three lines AB, CD and EF intersect at a point O such that ∠AOE=35∘ and ∠BOD=40∘. Find the measure of ∠AOC,∠BOF,∠COF and ∠DOE.
View SolutionTwo lines AB and CD intersect at point O. ∠AOD:∠BOD=3:1, then ∠AOD=…………………
View SolutionIn the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View Solutionstraight lines AB and CD intersect at O. If ∠AOC+∠BOD=130∘ then ∠AOD=?
View SolutionTwo lines AB and CD intersect at O. If ∠AOC=50∘, find ∠AOD,∠BOD and ∠BOC.
 View Solution
View Solution

