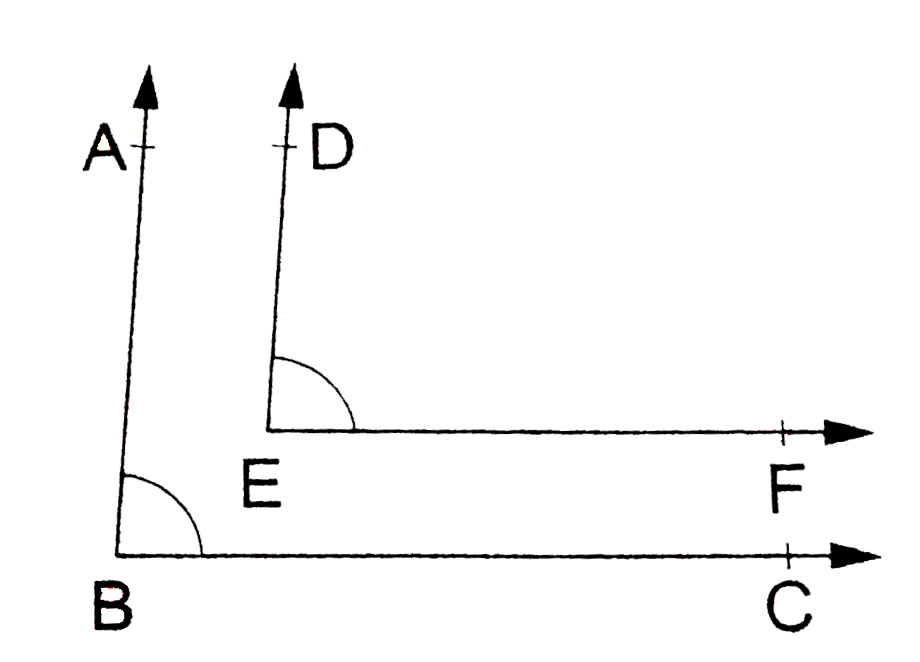
In the given figure, BA∣∣ED and BC∣∣EF. Show that ∠ABC=∠DEF.
Video Solution
Text Solution
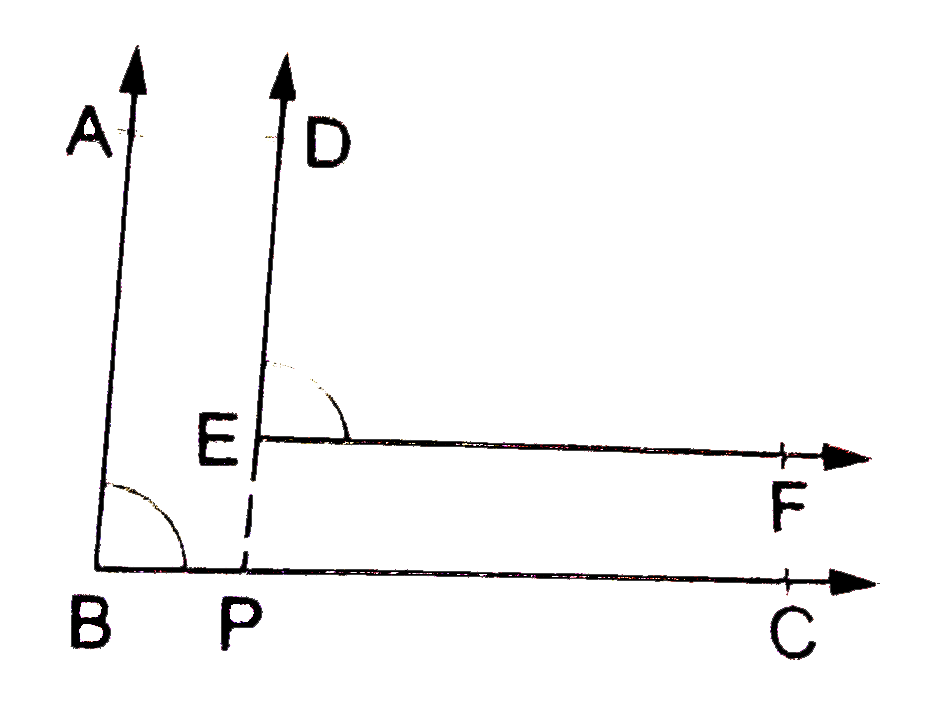
Product DE to meet BC at P.
BA∣∣PD and BPC is the transcersal.
∴∠ABC=∠DPC [corresponding ∠s]
EF∣∣BC and DP is the transversal.
∴∠DPC=∠DEF [corresponding ∠s].
Hence, ∠ABC=∠DEF.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure AB||CDandEF||DQ. Find the value of ∠DEF:
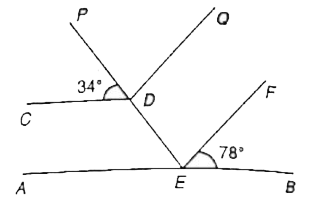 A68∘B78∘C34∘D39∘
A68∘B78∘C34∘D39∘ - Question 2 - Select One
In the ajoining figure AE∣∣CD and BC∣∣ED, then find y:
 A60∘B80∘C90∘D75∘
A60∘B80∘C90∘D75∘
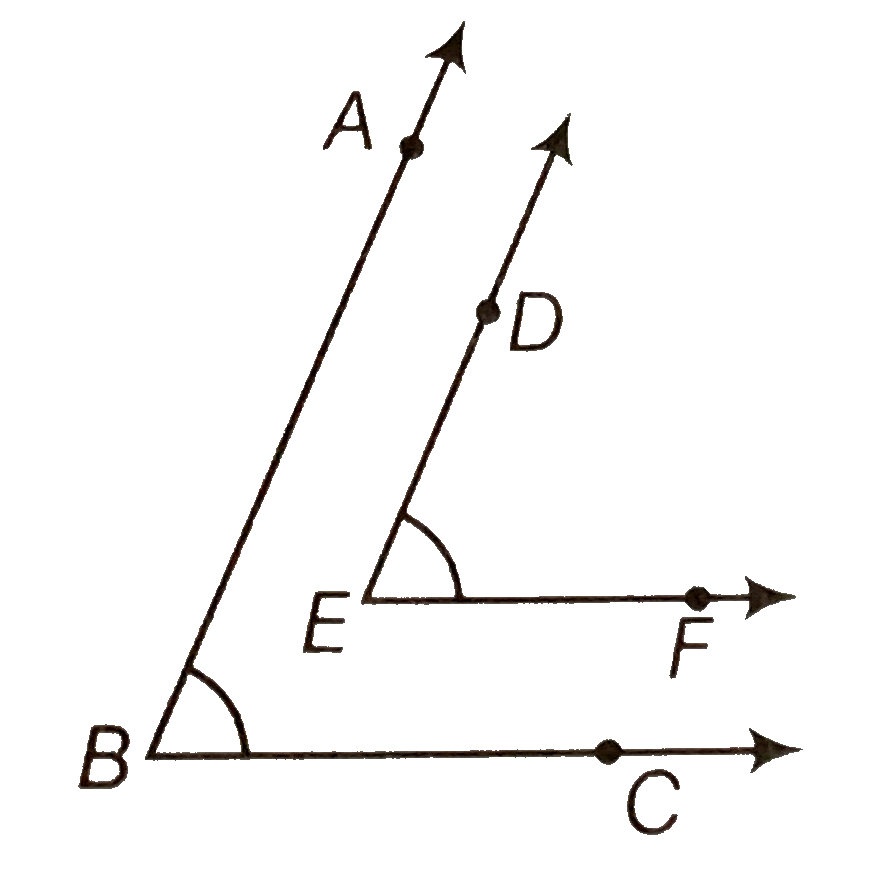
In the figure, BA|| ED and BC|| EF. Show that ∠ABC = ∠DEF.
 View Solution
View SolutionIn the given figure, AD⊥BCandCD>BD. Show that AC>AB.
 View Solution
View SolutionIn the given figure, ∠B<∠Aand∠C<∠D. Show that AD<BC.
View SolutionIn the given figure, AB∣∣DE. Prove that:
∠ABC+∠BCD=180∘+∠CDE.
 View Solution
View SolutionIn the given figure, AB||CD||EF. Find the value of x.
 View Solution
View SolutionIn the given figure , AB II ED and BC II EF , then the value of
∠ABC+∠DEF is :
 View Solution
View Solution


