A iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm heigh is surmounting it. Find the weight of the pillar, given that 1cm3 of iron weight 7.5 g
The correct Answer is:693 kg
To find the weight of the iron pillar, we need to calculate the volume of both the cylindrical portion and the conical portion, and then use the density of iron to find the weight.
1. Convert Measurements to Consistent Units:
- The height of the cylindrical portion is given as 2.8 m, which we convert to centimeters:
2.8m=2.8×100=280cm
- The diameter of the cylinder is 20 cm, so the radius r is:
r=202=10cm
- The height of the conical portion is given as 42 cm.
2. Calculate the Volume of the Cylinder:
- The formula for the volume V of a cylinder is:
V=πr2h
- Substituting the values:
Vcylinder=π(10)2(280)=π(100)(280)=28000πcm3
3. Calculate the Volume of the Cone:
- The formula for the volume V of a cone is:
V=13πr2h
- Substituting the values:
Vcone=13π(10)2(42)=13π(100)(42)=1400πcm3
4. Calculate the Total Volume of the Pillar:
- The total volume Vtotal is the sum of the volumes of the cylinder and the cone:
Vtotal=Vcylinder+Vcone=28000π+1400π=29400πcm3
5. Calculate the Weight of the Pillar:
- Given that 1 cm³ of iron weighs 7.5 g, the total weight W of the pillar can be calculated as:
W=Vtotal×weight per cm3=29400π×7.5g
- Approximating π≈3.14:
W≈29400×3.14×7.5
W≈29400×23.55≈692370g
6. Convert Weight to Kilograms:
- Since 1000 g = 1 kg, we convert the weight:
W≈6923701000≈692.37kg
Final Answer:
The weight of the iron pillar is approximately 692.37 kg.
- The height of the cylindrical portion is given as 2.8 m, which we convert to centimeters:
2.8m=2.8×100=280cm
- The diameter of the cylinder is 20 cm, so the radius r is:
r=202=10cm
- The height of the conical portion is given as 42 cm.
- The formula for the volume V of a cylinder is:
V=πr2h
- Substituting the values:
Vcylinder=π(10)2(280)=π(100)(280)=28000πcm3
- The formula for the volume V of a cone is:
V=13πr2h
- Substituting the values:
Vcone=13π(10)2(42)=13π(100)(42)=1400πcm3
- The total volume Vtotal is the sum of the volumes of the cylinder and the cone:
Vtotal=Vcylinder+Vcone=28000π+1400π=29400πcm3
- Given that 1 cm³ of iron weighs 7.5 g, the total weight W of the pillar can be calculated as:
W=Vtotal×weight per cm3=29400π×7.5g
- Approximating π≈3.14:
W≈29400×3.14×7.5
W≈29400×23.55≈692370g
- Since 1000 g = 1 kg, we convert the weight:
W≈6923701000≈692.37kg
The weight of the iron pillar is approximately 692.37 kg.
Topper's Solved these Questions
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Exercise 15D
28 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Exercise 15B
33 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
An iron pillar consists of a cylindrical portion of 2.8m. height and 20cm. in diamea cone of 42cm. height surmounting it. Find the weight of the pillar if 1cm3 of iron weights 7.5g.
View SolutionAn iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use π=355/115 )
View Solution
Knowledge Check
An iron pillar has some part n the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of cone , as well as cylinder is 21 cm . The cylindrical part is 80 cm high and conical part is 16 cm high . Find the weight of the pillar , if 1cm3 of iron weighs 8.45 g :
A999.39 kgB111 kgC1001 kgD989 kgAn iron pillar has some part n the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of cone , as well as cylinder is 21 cm . The cylindrical part is 80 cm high and conical part is 16 cm high . Find the weight of the pillar , if 1cm3 of iron weighs 8.45 g :
A999.39 kgB111 kgC1001 kgD989 kgAn iron pillar has some part in the from of right circular cylinder and the remaining in the from of a right circular cone .The radius of the base of each of the cone and the cylinder is 8 cm . The cylindrical part is 240 cm hight and the conical part is 36 cm hight .Find the weight of the pillar if 1 cubic centimetre of iron weighs 7.5 g .
A480. 16 kgB380.16kgC580. 16 kgD680. 16 kg
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1cm3 of iron has approximately 8 gm mass. (Use ∏ = 3.14)
View SolutionA solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass (Use π=3.14 )
View SolutionAn iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find
(i) The volume of iron used
(ii) The weight of pillar, if 1 cm3 of iron weighs 10g.
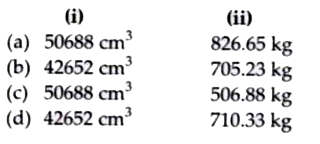
View SolutionAn iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weighs 7.8 grams.
View SolutionA solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3of iron has approximately 8g mass.
View Solution