The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
35∘
38∘
40∘
45∘
The correct Answer is:B
To solve the problem, we will use the properties of a parallelogram and the relationships between the angles formed by the diagonals.
1. Identify the Given Angles:
- We are given that ∠DAC=32∘ and ∠AOB=70∘.
2. Use the Property of Parallelogram:
- In a parallelogram, the diagonals bisect each other. Therefore, AO=OC and BO=OD.
3. Find ∠AOD:
- Since ∠AOB=70∘, and ∠AOB and ∠AOD are vertically opposite angles, we have:
∠AOD=∠AOB=70∘
4. Find ∠DAC+∠DAB:
- In triangle AOD, the sum of angles is 180∘:
∠DAC+∠DAB+∠AOD=180∘
- Let ∠DAB=x. Therefore, we can write:
32∘+x+70∘=180∘
- Simplifying this gives:
x+102∘=180∘
- Thus,
x=180∘−102∘=78∘
- Therefore, ∠DAB=78∘.
5. Find ∠DBC:
- Since AB∥CD (as it is a property of parallelograms), we have:
∠DAB=∠DBC
- Therefore, ∠DBC=78∘.
Final Answer:
∠DBC=78∘
- We are given that ∠DAC=32∘ and ∠AOB=70∘.
- In a parallelogram, the diagonals bisect each other. Therefore, AO=OC and BO=OD.
- Since ∠AOB=70∘, and ∠AOB and ∠AOD are vertically opposite angles, we have:
∠AOD=∠AOB=70∘
- In triangle AOD, the sum of angles is 180∘:
∠DAC+∠DAB+∠AOD=180∘
- Let ∠DAB=x. Therefore, we can write:
32∘+x+70∘=180∘
- Simplifying this gives:
x+102∘=180∘
- Thus,
x=180∘−102∘=78∘
- Therefore, ∠DAB=78∘.
- Since AB∥CD (as it is a property of parallelograms), we have:
∠DAB=∠DBC
- Therefore, ∠DBC=78∘.
∠DBC=78∘
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXAMPLE
32 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DPBAP.BP = CP. DPCAP. CD = AB. CPDBP. AB = CD.CP
The diagonals Ac and BD of a parallelogram intersects at O. If ∠OAD=40∘,∠OAB=20∘and∠COD=75∘, then evaluate the following,
∠ABD
View SolutionThe diagonals Ac and BD of a parallelogram intersects at O. If ∠OAD=40∘,∠OAB=20∘and∠COD=75∘, then evaluate the following,
∠BDC
View SolutionThe diagonals AC and BD of a parallelogram intersects at O. If ∠OAD=40∘,∠OAB=20∘and∠COD=65∘, then evaluate the following,
∠DBC
View SolutionThe diagonals Ac and BD of a parallelogram intersects at O. If ∠OAD=40∘,∠OAB=20∘and∠COD=75∘, then evaluate the following,
∠ADC
View SolutionIn fig., ABCD is a cyclic quadrilatreral. If ∠BAC=50∘ and ∠DBC=60∘, then find ∠BCD.
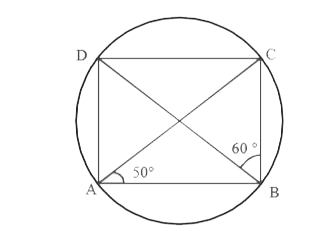
View Solution