ABCD is a rhombus in which the altitude from D to side AB bisects AB. Find the angles of the rhombus.
Video Solution
Text Solution
The correct Answer is:60∘,120∘,60∘,120∘
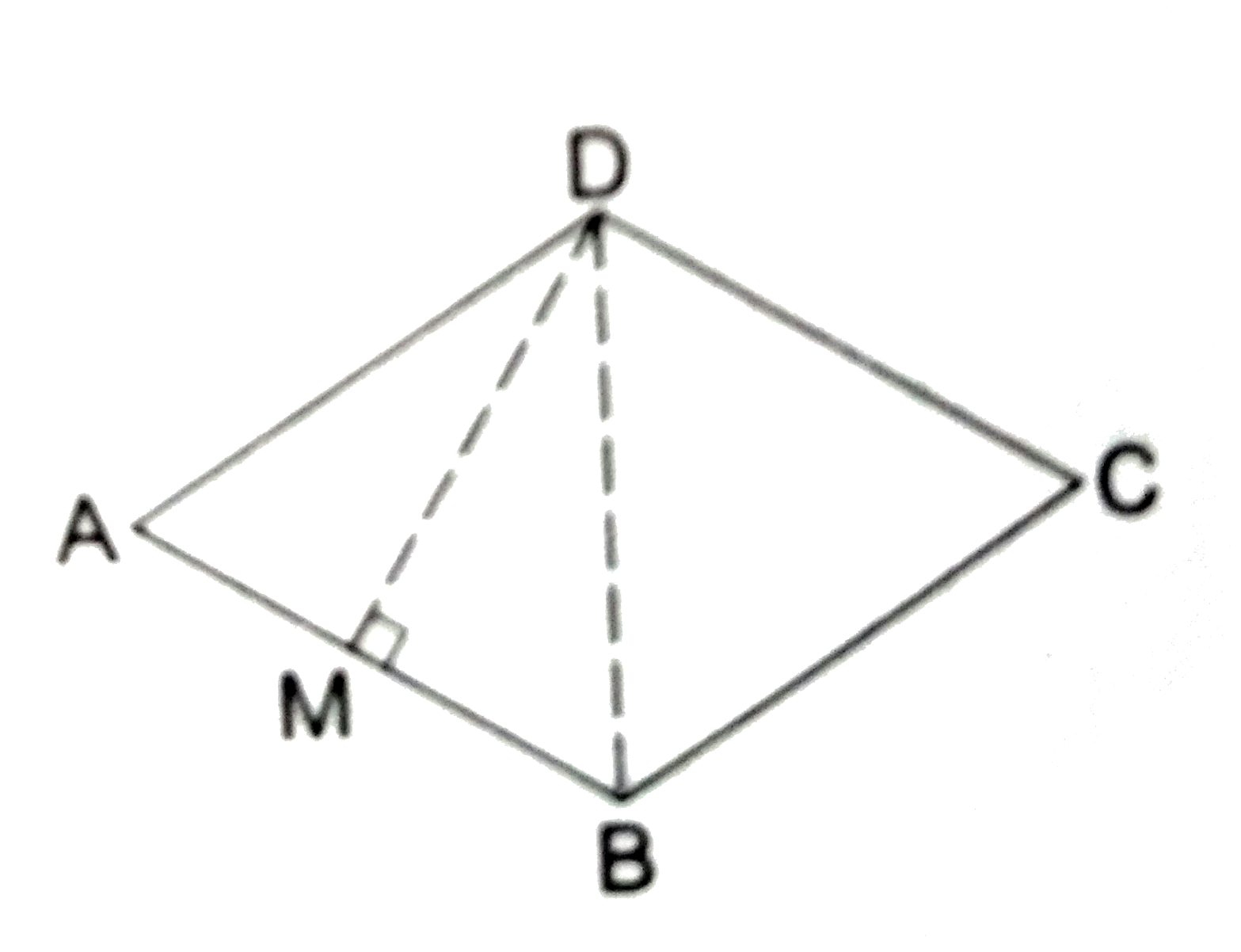
DM⊥ABandAM=MB.
△AMD≅△BMD
(∵AM=MB,∠AMD=∠BMD=90∘,DM=DM).
∴AB=AD=DB⇒△ABD is equilateral.
So, ∠A=60∘⇒∠B=120∘,∠C=60∘,∠D=120∘.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a rhombus in which altitude from point D to the side AB bisects AB. The angles of the rhombus are :
A150∘,30∘,150∘,30∘B135∘,45∘,135∘,45∘C1161∘3,632∘3,1161∘3,622∘3D120∘,60∘,120∘,60∘ - Question 2 - Select One
One of the diagonals of a rhombus is equal to a side of the rhombus. The pair of unequal angles of the rhombus are
A60∘,80∘B60∘,120∘C120∘,240∘D100∘,120∘
One of the diagonals of a rhombus is equal to one of its sides. Find the angles of the rhombus.
View SolutionABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then Δ ABD is equilateral.View SolutionOne of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.
View SolutionEFGH is a rhombus. Find a, b, c
View SolutionDiagonal AC of a rhombus ABCD is a equal to one of its sides BC. Find all the angles of the rhombus.
 View Solution
View SolutionIf ABCD is a rhombus with ∠ABC=56∘, find the measure of ∠ACD
View Solution

