Question

The diagonals of a quadrilateral ABCD are equal. Prove that the quardilateral formed by joining the midpoints of its sides is a rhombus.

Explanation

To prove that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD (where the diagonals AC and BD are equal) is a rhombus, we will follow these steps:

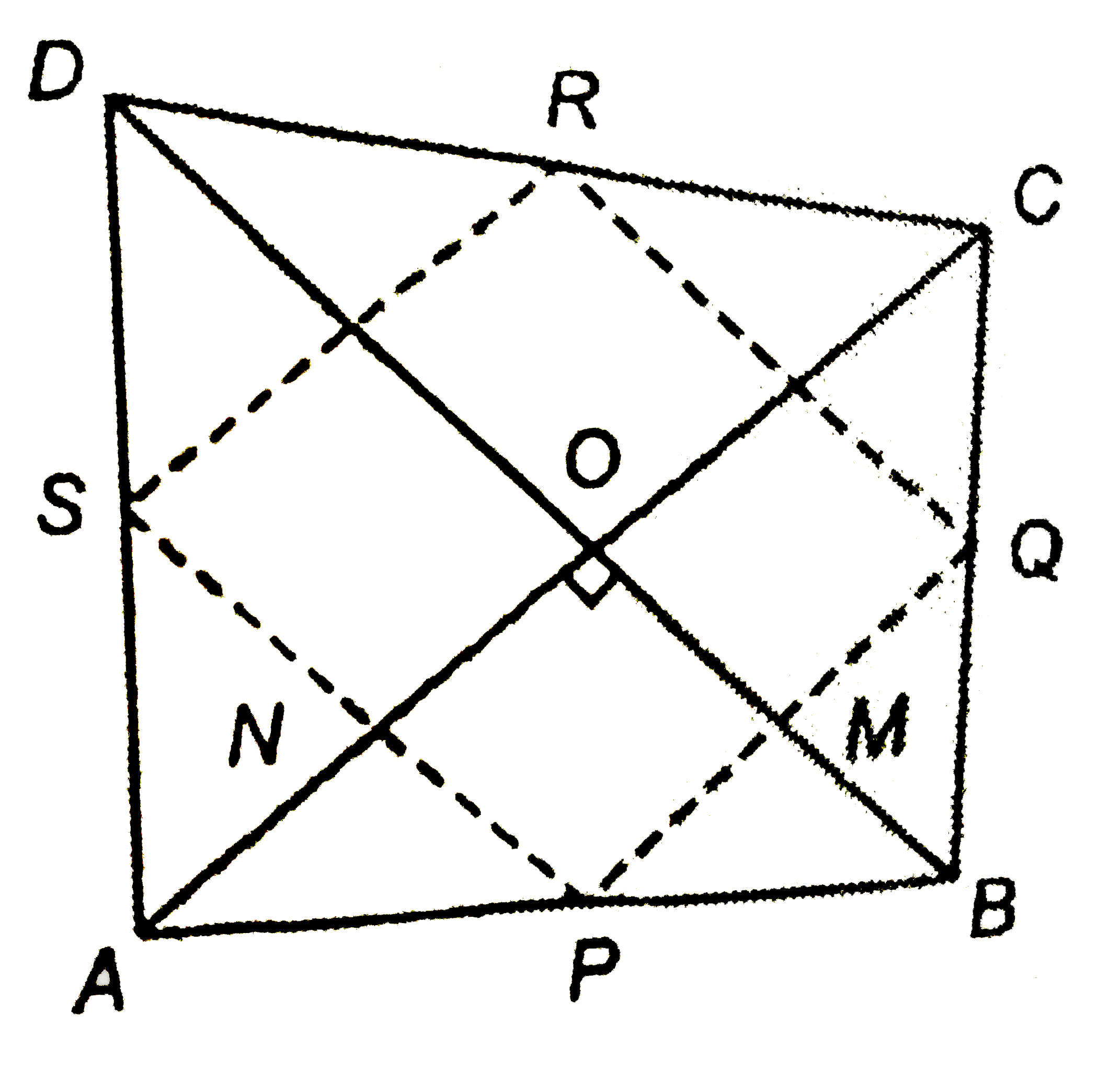
1. Draw Quadrilateral ABCD:
- Start by sketching quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- Label the midpoints of sides AB, BC, CD, and DA as P, Q, R, and S respectively.

2. Identify Midpoints:
- Let P be the midpoint of AB, Q be the midpoint of BC, R be the midpoint of CD, and S be the midpoint of DA.

3. Apply the Midpoint Theorem:
- According to the midpoint theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
- In triangle ABC:
- Since P and Q are midpoints, PQ is parallel to AC and PQ = 1/2 * AC.

4. Consider Triangle BCD:
- In triangle BCD:
- Q and R are midpoints, so QR is parallel to BD and QR = 1/2 * BD.

5. Consider Triangle ACD:
- In triangle ACD:
- S and R are midpoints, so SR is parallel to AC and SR = 1/2 * AC.

6. Consider Triangle ABD:
- In triangle ABD:
- P and S are midpoints, so PS is parallel to BD and PS = 1/2 * BD.

7. Establish Parallel Sides:
- From the above steps, we have:
- PQ || RS (since both are parallel to AC)
- QR || PS (since both are parallel to BD)

8. Show Opposite Sides are Equal:
- Since AC = BD (given), we can conclude:
- PQ = 1/2 * AC and SR = 1/2 * AC, thus PQ = SR.
- QR = 1/2 * BD and PS = 1/2 * BD, thus QR = PS.

9. Conclude that Opposite Sides are Equal:
- We have established that:
- PQ = SR and QR = PS.
- Therefore, opposite sides of quadrilateral PQRS are equal.

10. Conclude that PQRS is a Rhombus:
- Since opposite sides are equal and parallel, quadrilateral PQRS is a rhombus.

Final Conclusion:
Thus, we have proved that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD is a rhombus.

---