Look at the statement given below:
I. A parellelogram and a rectangle on the same base and between the same parallels are equal in area.
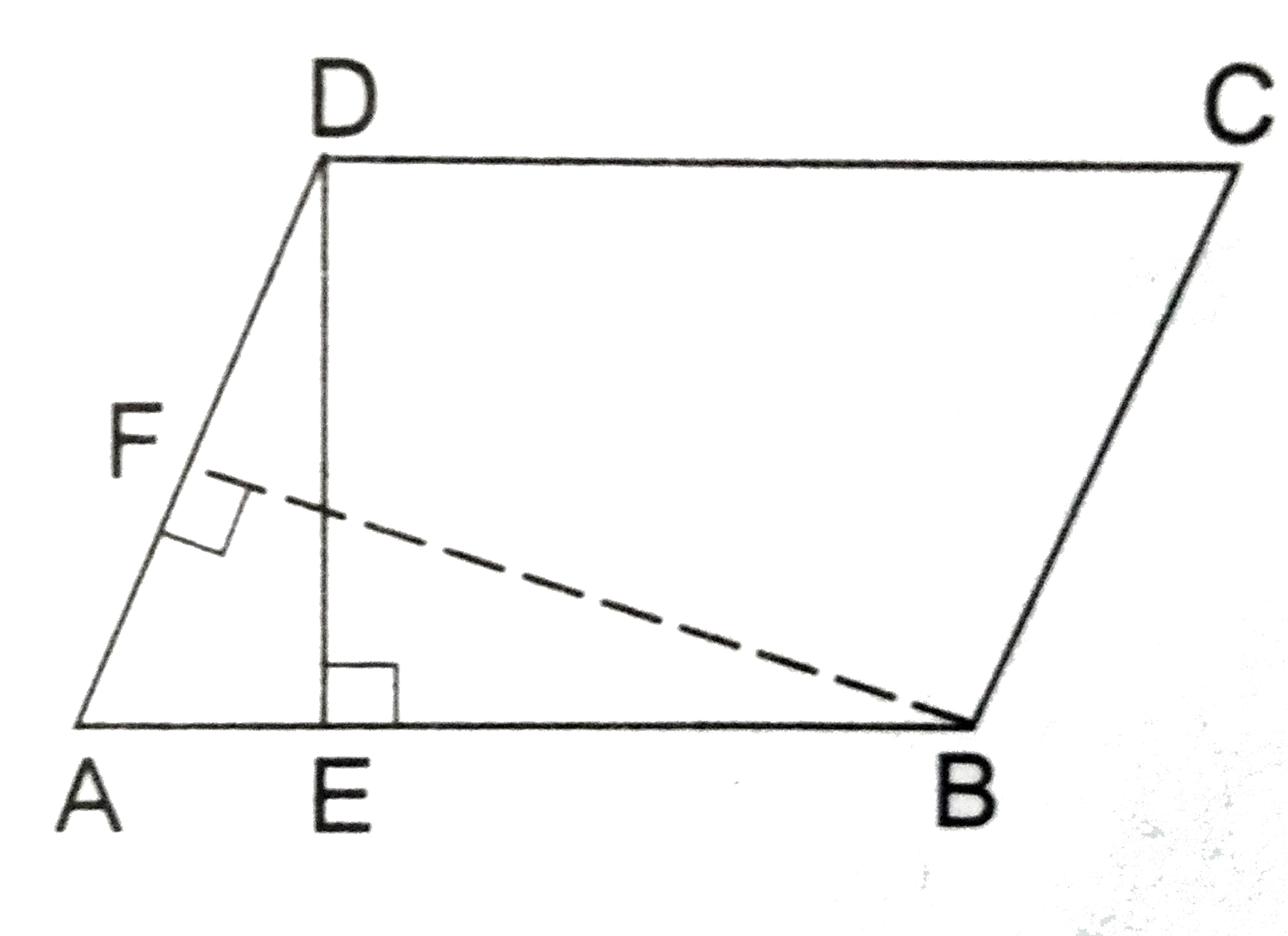
II. In a ||gm ABCD, it is given that AB = 10 cm. The altitudes DE and AB and BF on AD being 6 cm and 8 cm respectively, then AD = 7.5 cm.
III. Area of a ||gm =12×base×altitude.
Which is true?
I only
II only
I and II
II and III
The correct Answer is:C
Clearly I is true.
AB×DE=(10×6)and(AD×BF)=(7.5×8)=60
∴ II is true.
But, III is clear false,as we know that
area of a ||gm = base × altitude.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 1138videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , Ad is the bisector of ∠BAC. If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .
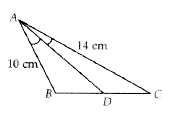 A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm - Question 2 - Select One
In the given figure, ABCD is a ||gm in which DL⊥AB. IF AB = 10 cm and DL = 4 cm then the ar(||gm ABCD) = ?
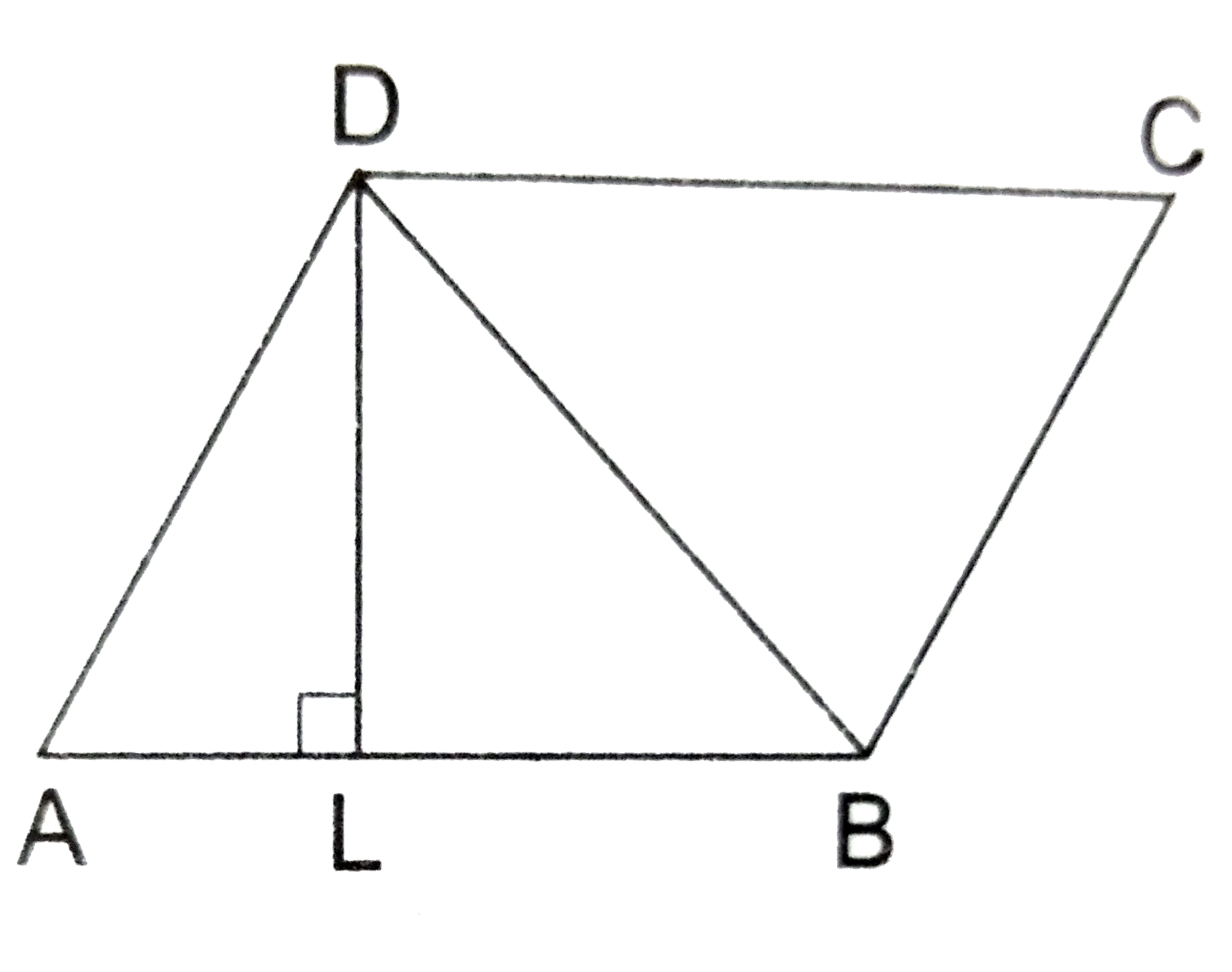 A40cm2B80cm2C20cm2D196cm2
A40cm2B80cm2C20cm2D196cm2
In a parallelogram ABCD, it is being given that AB = 10 cm and the altitudes corresponding to the sides AB and AD are DL = 6 cm and BM = 8 cm, respectively. Find AD.
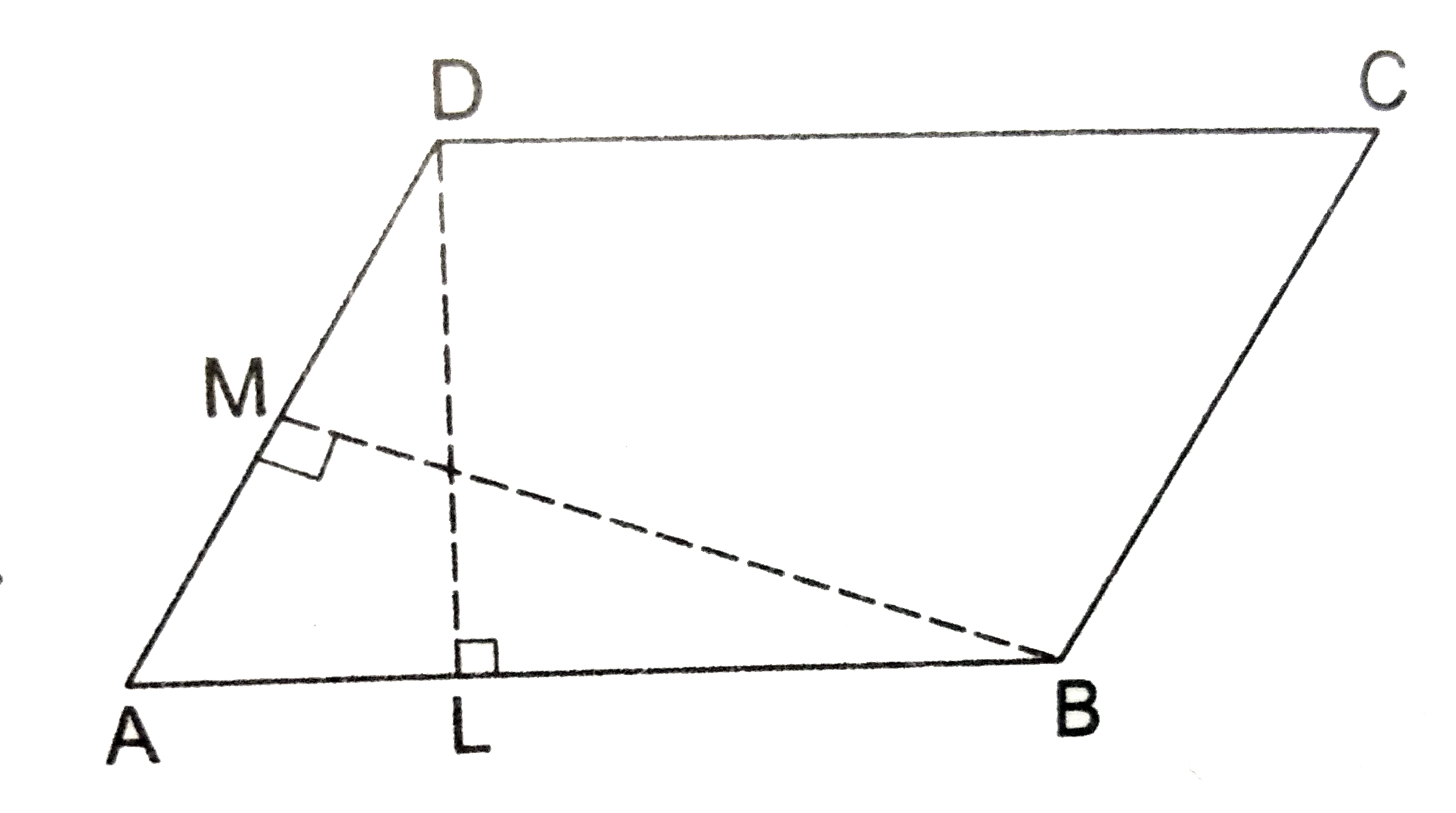 View Solution
View SolutionIn parallelogram ABCD, AB = 10 cm. The altitudes corresponding to the sides AB and AD are respectively 7 cm and 8 cm. If AD is k cm. Then value of 4 k is
View SolutionIn parallelogram ABCD,AB=10cm. The altitudes corresponding to the sides AB and AD are respectively 7cm and 8cm. Find AD.
View SolutionABCD is a rectangle with AB=8cmandAD=6cm. The bisector of internal angle of BandD meet the diagonal AC in PandQ repectively, then
View SolutionIn a ΔABC, if DE is drawn parallel to BC, cutting AB and AC to D and E respectively such that AB=7.2cm,AC=6.4cmandAD=4.5cm. Then, AE=?
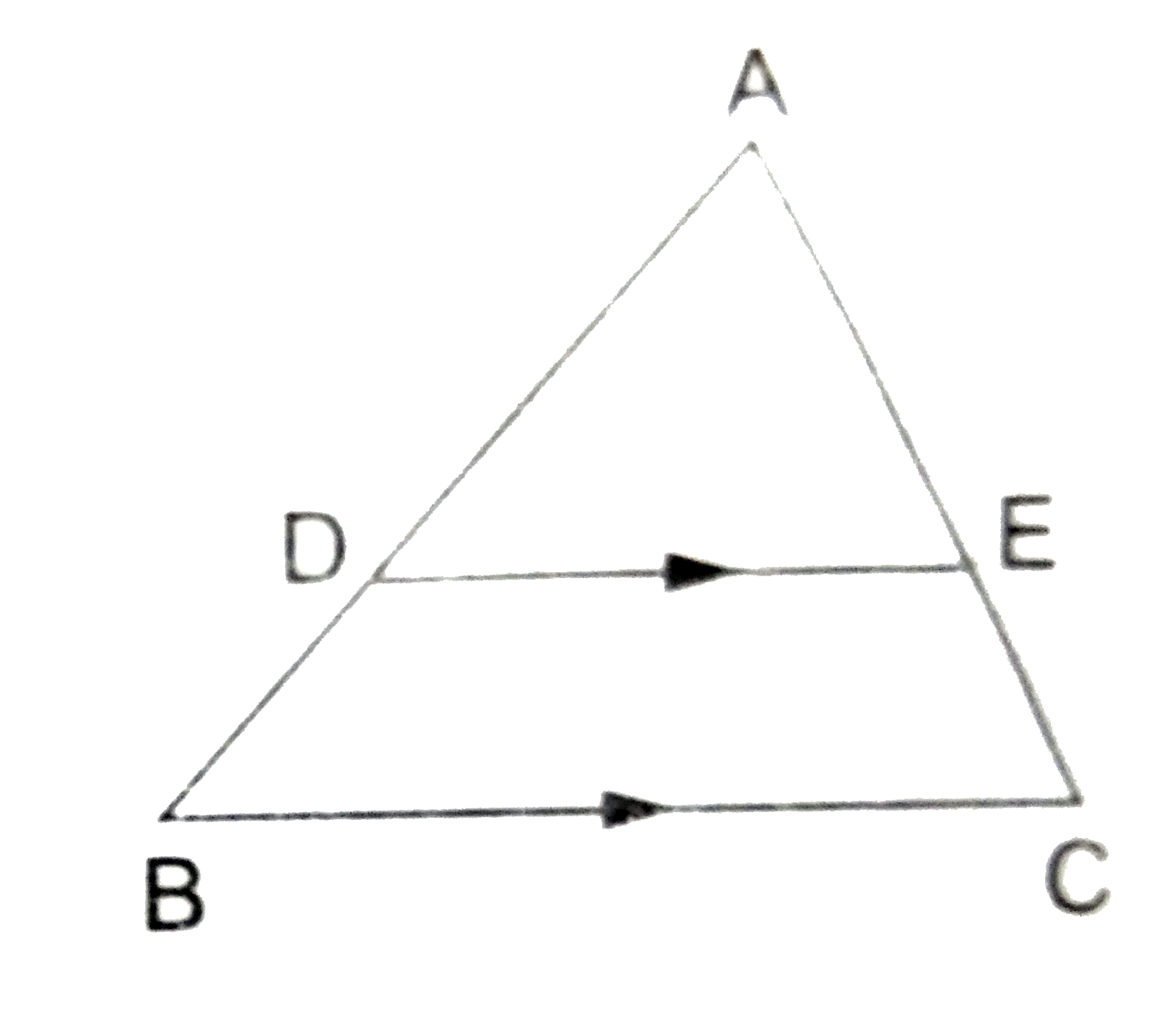 View Solution
View SolutionIn the figure given below, AC is parallel to ED and AB = DE = 5 cm and BC = 7 cm. What is the area ABDE : area BDE : area BCD equal to ?
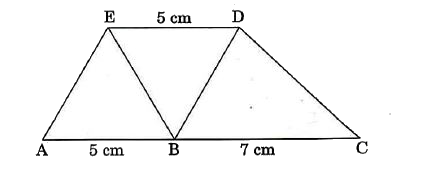 View Solution
View Solution

