Two tangent segments $B C$ and $B D$ are drawn to a circle with centre $O$ such that $∠ C B D = 120^{\circ}$ . Prove that $O B = 2 B C$ .

Video Solution

Answer

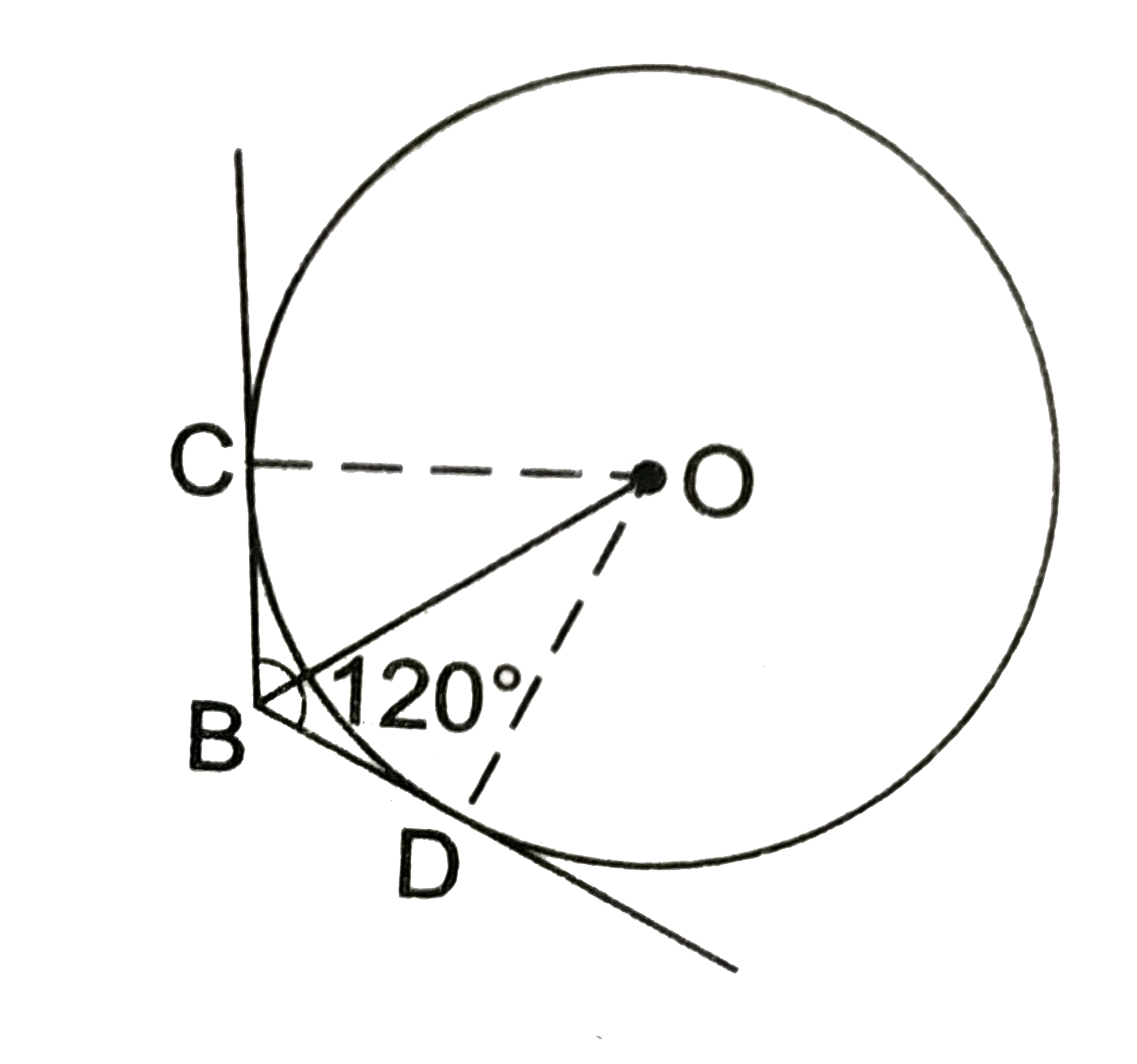
Step by step video & image solution for Two tangent segments BC and BDare drawn to a circle with centre O such that /_CBD=120^(@). Prove that OB=2BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason
1 Videos
ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos

Knowledge Check

If PA and PB are two tangents to a circle with centre O such that $∠ A P B = 80^{\circ}$ , then, $∠ A O P = ?$
A $40^{\circ}$
B $50^{\circ}$
C $60^{\circ}$
D $80^{\circ}$
If PQ and PR be the two tangents to a circle with centre O such that $∠ Q P R = 120^{\circ}$ then $∠ P O Q$ is
A $90^{\circ}$
B $45^{\circ}$
C $30^{\circ}$
D $60^{\circ}$
Two tangents PA and PB are drawn to a circle of centre O in such a way that $∠ A O B = 120^{\circ}$ . Calculate the value of $∠ A P B$ .

A40°
B50°
C60°
D80°

RS AGGARWAL-CIRCLES-Test Yourself

Home
Ask Doubt
Profile

Two tangent segments BC and BDare drawn to a circle with centre O such that ∠CBD=120∘. Prove that OB=2BC.

Topper's Solved these Questions

Similar Questions

Knowledge Check

If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?

If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is

Two tangents PA and PB are drawn to a circle of centre O in such a way that ∠AOB=120∘. Calculate the value of ∠APB.

RS AGGARWAL-CIRCLES-Test Yourself

Two tangent segments $B C$ and $B D$ are drawn to a circle with centre $O$ such that $∠ C B D = 120^{\circ}$ . Prove that $O B = 2 B C$ .

If PA and PB are two tangents to a circle with centre O such that $∠ A P B = 80^{\circ}$ , then, $∠ A O P = ?$

If PQ and PR be the two tangents to a circle with centre O such that $∠ Q P R = 120^{\circ}$ then $∠ P O Q$ is

Two tangents PA and PB are drawn to a circle of centre O in such a way that $∠ A O B = 120^{\circ}$ . Calculate the value of $∠ A P B$ .