3x+2y≤12,x≥1,y≥2
To solve the given linear inequalities and graph the feasible region, we will follow these steps:
Step 1: Write down the inequalities
We have the following inequalities:
1. 3x+2y≤12
2. x≥1
3. y≥2
Step 2: Convert the first inequality into an equation
To graph the line represented by the first inequality, we convert it into an equation:
3x+2y=12
Step 3: Find the intercepts of the line
To find the x-intercept, set y=0:
3x+2(0)=12⟹3x=12⟹x=4
So, the x-intercept is (4,0).
To find the y-intercept, set x=0:
3(0)+2y=12⟹2y=12⟹y=6
So, the y-intercept is (0,6).
Step 4: Plot the line on the coordinate axis
Now, we plot the points (4,0) and (0,6) on the graph and draw a line through these points. Since the inequality is ≤, we will use a solid line.
Step 5: Determine the region for the first inequality
To find which side of the line satisfies the inequality 3x+2y≤12, we can test a point not on the line, such as the origin (0,0):
3(0)+2(0)=0≤12(True)
This means the region including the origin is part of the solution.
Step 6: Graph the other inequalities
Now we graph the other inequalities:
1. For x≥1, draw a vertical dashed line at x=1 and shade to the right.
2. For y≥2, draw a horizontal dashed line at y=2 and shade above.
Step 7: Identify the feasible region
The feasible region is where all shaded areas overlap. This will be a triangular region bounded by:
- The line 3x+2y=12
- The vertical line x=1
- The horizontal line y=2
Step 8: Conclusion
The feasible region represents all the solutions to the given inequalities.
We have the following inequalities:
1. 3x+2y≤12
2. x≥1
3. y≥2
To graph the line represented by the first inequality, we convert it into an equation:
3x+2y=12
To find the x-intercept, set y=0:
3x+2(0)=12⟹3x=12⟹x=4
So, the x-intercept is (4,0).
3(0)+2y=12⟹2y=12⟹y=6
So, the y-intercept is (0,6).
Now, we plot the points (4,0) and (0,6) on the graph and draw a line through these points. Since the inequality is ≤, we will use a solid line.
To find which side of the line satisfies the inequality 3x+2y≤12, we can test a point not on the line, such as the origin (0,0):
3(0)+2(0)=0≤12(True)
This means the region including the origin is part of the solution.
Now we graph the other inequalities:
1. For x≥1, draw a vertical dashed line at x=1 and shade to the right.
2. For y≥2, draw a horizontal dashed line at y=2 and shade above.
The feasible region is where all shaded areas overlap. This will be a triangular region bounded by:
- The line 3x+2y=12
- The vertical line x=1
- The horizontal line y=2
The feasible region represents all the solutions to the given inequalities.
Topper's Solved these Questions
- LINEAR INEQUATIONS (IN TWO VARIABLES )BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN TWO VARIABLES )EXERCISE - EXERCISE 7
22 Videos
- LINEAR INEQUATIONS (IN ONE VARIABLE)BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN ONE VARIABLE)EXERCISE - EXERCISE 6B
12 Videos
- LogarithmBOOK - RS AGGARWALCHAPTER - LogarithmEXERCISE - Exercise 1
9 Videos
Similar Questions
Knowledge Check
The solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
A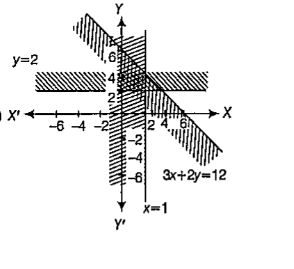 B
B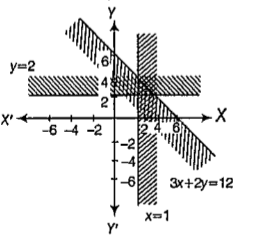 C
C DNone of the above
DNone of the above
Minimise Z=−3x+4y
subject to x+2y≤8,3x+2y≤12,x≥0,y≥0.
View SolutionZ=−3x+4y
x+2y≤8,3x+2y≤12,x≥0,y≥0
View SolutionZ=−3x+4y
x+2y≤8,3x+2y≤12,x≥0,y≥0.
View Solution(a) Draw the feasible region of inequation:
x+y≤4,x≥0,y≥0
(b) Draw the graph of the following LPP:
3x+y≤17,x,y≥0
(c) Shade the feasible region of LLP:
(i) x+3y≥3,x+y≥2,x≥0,y≥0
(ii) x+2y≤8,3x+2y≤12,x≥0,y≥0
View SolutionMaximize z=5x+10y subject to constraints x+2y≤10,3x+y≤12,x≥0,y≥0
View SolutionMaximize z=2x+3y subject to constraints x+4y≤8,3x+2y≤14,x≥0,y≥0.
View SolutionZ=13x+3y
x+y≤6,3x+2y≤15,x≥0,y≥0.
View Solution
