Find the coefficient of x4 in the expansion of (1+x)n(1−x)n. Deduce that C2=C0C4−C1C3+C2C2−C3C1+C4C0, where Cr stands for nCr.
The correct Answer is:C2
(1+x)n×(1−x)n=[C0+C1x+C2x2+...+Cnxn]×[C0−C1x+C2x2−...+(−1).nCnxn]
(1+x)n×(1−x)n=(1−x2)n=[C0−C1x2+C2x4−...+(−1).nCnx2n]
∴C0C4−C1C3+C2C2−C3C1+C4C0=C2.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 11F (Very Short-Answer Type Questions)17videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B18videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
If C0,C1C2 ….., denote the binomial coefficients
in the expansion of (1+x)n , then
C02−C13+C24−C35+...+(−1)nCnn+2=A1n+1B1n+2C1n(n+1)D1(n+1)(n+2)
Prove that C0–22C1+3²C2–42C3+...+(−1)n(n+1)2Cn=0 where Cr=nCr
View SolutionFind the coefficient of xn in the polynomial (x+nC0)(x+3nC1)×(x+5nC2)[x+(2n+1)nCn].
View SolutionProve that C0−22C1+32C2−42C3++(−1)n(n+1)2×Cn=0whereCr=nCr .
View SolutionIn C_(0),C_(1)C_(2)….C_(n) are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
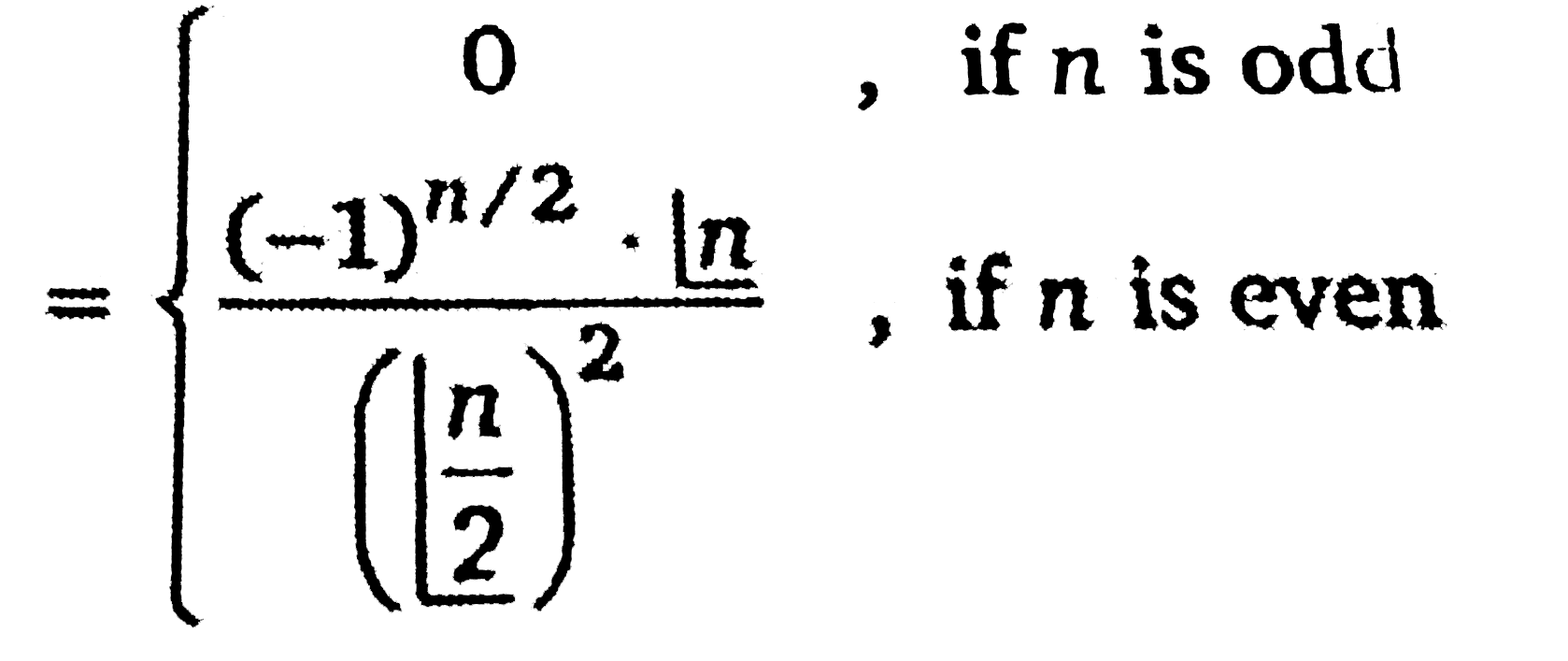
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
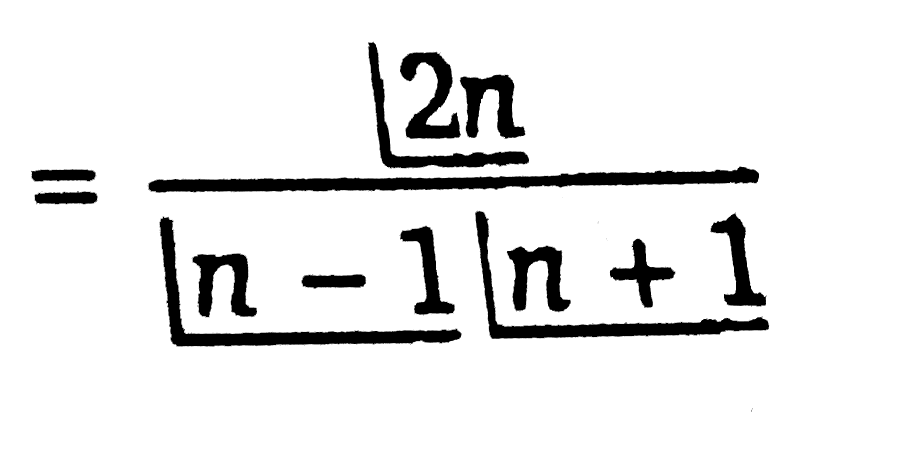 View Solution
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
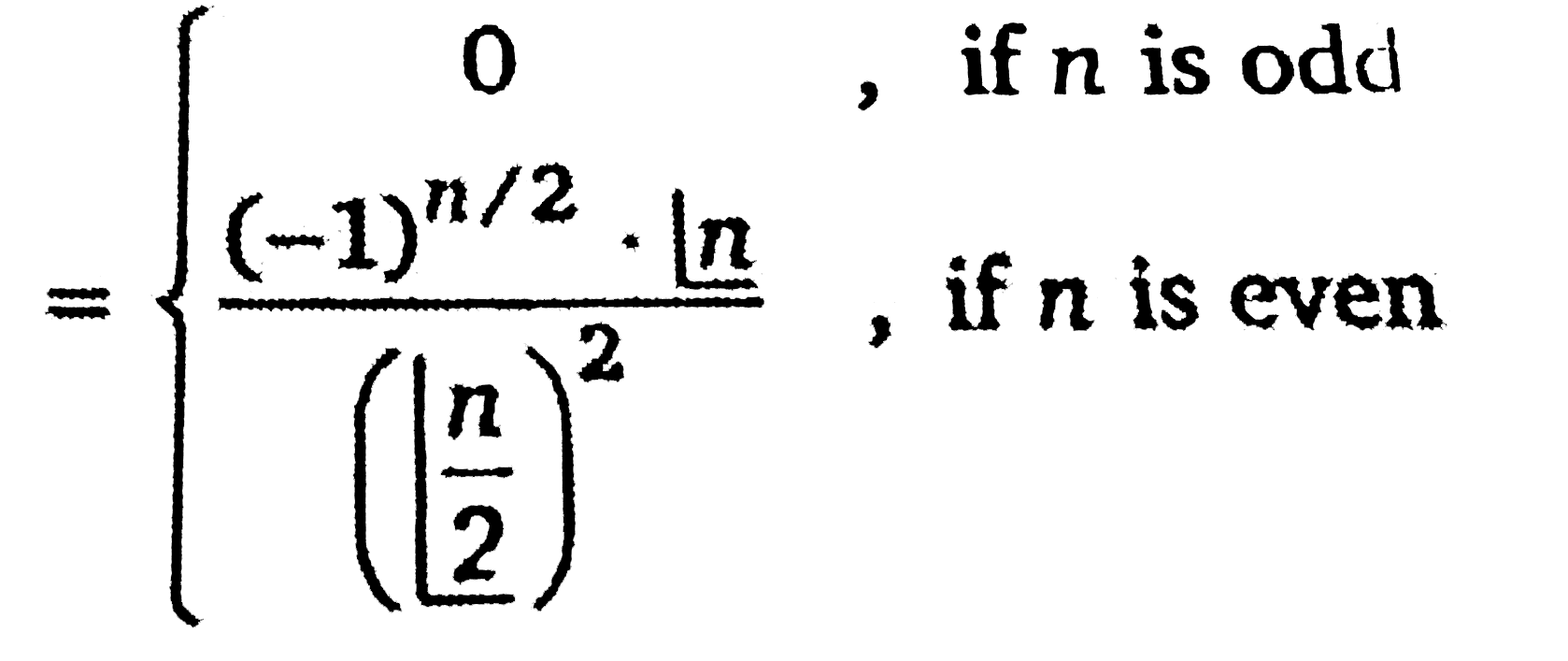
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
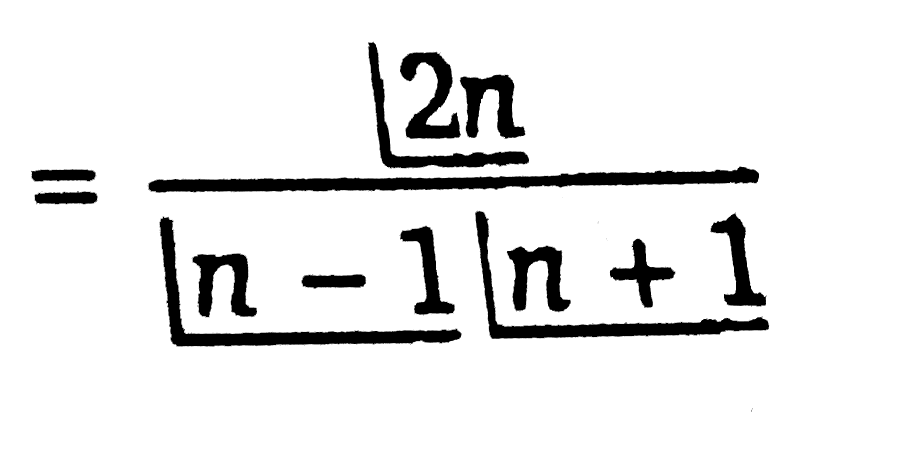 View Solution
View SolutionIf C0,C1,C2,..........Cn, are the Binomial coefficients in the expansion of (1+x)n, n being even, then C0+(C0+C1)+(C0+C1+C2)+.....+(C0+C1+C2+.......+Cn−1) is equal to
View SolutionIfC0,C1,C2..Cn denote the coefficients in the binomial expansion of (1+x)n, then C0+2.C1+3.C2+.(n+1)Cn
View Solution

