तीन संकेन्द्रीय धात्विक कोशो A, B और C की त्रिज्या क्रमशः a, b और c(a<b<c) है जिनके पृष्ठ आवेश घनत्व क्रमशः +σ,−σ और +σ है तो कोश B पर विभव का मान होगा
σε0[a2−b2a+c]
σε0[a2−b2b+c]
σε0[b2−c2b+a]
σε0[b2−c2c+a]
The correct Answer is:B
संकेत B पर विभव = आवेश के कारण A पर विभव + आवेश के कारण B पर विभव + आवेश के कारण C पर विभव
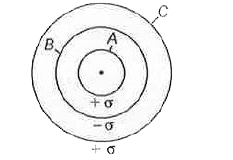
∴VB=k(QA+QB)b+kQcc
=14πε0[σ4πa2b−σ4πb2b+σ4πc2c]
=σε0(a2−b2b+c2c)=σε0(a2−b2b+c)
VB=σε0(a2−b2b+c)
Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - सॉल्वड पेपर 2015 JEE MAIN संयुक्त प्रवेश परीक्षा EXERCISE - भौतिकी30videos
सॉल्वड पेपर 2015 JEE MAIN संयुक्त प्रवेश परीक्षा
- BOOK - ARIHANT HINDICHAPTER - सॉल्व्ड पेपर 2014 JEE MAIN संयुक्त प्रवेश परीक्षा EXERCISE - प्रश्न30videos
सॉल्व्ड पेपर 2014 JEE MAIN संयुक्त प्रवेश परीक्षा
Similar Questions
किसी 240 मी ऊँची चोटी के एक किनारे से, दो पत्थरों को एक साथ ऊपर की ओर फेंका गया है। इनकी प्राथमिक चाल क्रमशः 10 मी/से तथा 40 मी/से है। निम्नांकित में से कौन - सा ग्राफ (आरेख) पहले पत्थर के सापेक्ष दूसरे पत्थर की स्थिति के समय विचरण (परिवर्तन) को सर्वाधिक सही दर्शाता है ? (मान लीजिए कि, पत्थर जमीन से टकराने के पश्चात् ऊपर की ओर नहीं उछलते है तथा वायु का प्रतिरोध नगण्य है, दिया है g = 10 मी/से2) (यहाँ ग्राफ केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)
06:47View Solutionएक डायोड की धारा-वोल्टता सम्बन्ध I=(e1000V/T−1) मिली-ऐम्पियर दिया गया है। जहाँ लगाई गई वोल्टता V वोल्ट में है और तापमान T केल्विन में है। यदि एक विद्यार्थी 300 K पर 5 मिली-ऐम्पियर धारा मापते समय ±0.01V की त्रुटि करता है, तब धारा के मान में मिली-ऐम्पियर में होने वाली त्रुटि क्या होगी?
09:35View SolutionThree concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.
08:39View Solutionतीन संकेन्द्री धातु कोष A , B तथा C जिनकी त्रिज्याये क्रमशः a , b तथा c(a<b<c) है, पृष्ठ -आवेश-घनत्व क्रमशः +σ,−σ तथा +σ है कोष B का विभव होगा :
04:57View Solutionएक चर समतल किसी नियत बिंदु(a ,b ,c ) से होकर गुजरता है और अक्षो को क्रमशः A ,B और C पर काटता है। गोलक OABC के केंद्र का बिन्दुपथ जहॉं O निर्देशक मूलबिंदु है , कौन-सा है ?
07:28View SolutionThree concentric metal shells A, B, and C of respective radii a,b and c (a lt b lt c) have surface charge densities +σ,−σand+σ respectively. The potential of shell B is
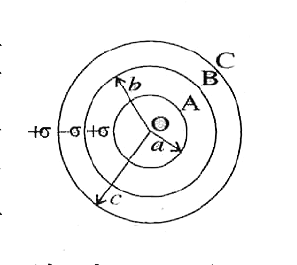
02:28View Solutionधातु के तीन संकेन्द्रीय कोशों A, B, C की त्रिज्याएँ क्रमशः a, b, c तथा हैं (a<b<c) तथा इनके आवेश के पृष्ठ धनत्व क्रमशः +σ,−σ,+σ हैं, जैसा कि चित्र में दिखाया गया है |
गोलीय कोश A का विभव ज्ञात कीजिए |
 08:04View Solution
08:04View Solutionयदि ω(≠1) इकाई का घनमूल है और (1+ω)7=A+Bω हो, तो A और B क्रमशः होंगे
04:22View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
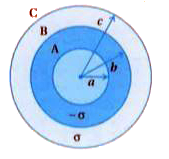
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.06:59View SolutionConsider A, D and C to be the co-centric shells of metal . Their radii are a ,b and c respectively (a < b < c). Their surface charge densities are σ,−σ and σ respectively. Calculate the electric potential on the surface of shell A.
 05:16View Solution
05:16View SolutionThree concentric spherical metallic spheres A,B and C of radii a,b and c(a<b<c) have surface charge densities σ,−σ and σ respectively.
07:10View SolutionThree concentric metallic spherical shell A,B and C or radii a,b and c(a<b<c) have surface charge densities −σ,+σand−σ. Respectively. The potential of shel A is :
01:18View Solutiona, b एवं c (a < b < c) त्रिज्या के तीन सकेन्द्रीय धात्विक कोष के पृष्ठ आवेश घनत्व क्रमशः −σ,+σ एवं −σ है। कोष A पर विभव होगा।
01:40View SolutionIf A is 40% less than B and C is 40 % of the sum of A and B, then by what percentage is B greater than C?
यदि A, B और C से 40% कम है, तो A और B के योग का 40% है, तो B, C से कितने प्रतिशत अधिक है?01:14View SolutionA sum of Rs. x is divided among A, B and C such that the ratio of the shares of A and B is 6:7 and that of B and C is 3:2. If the difference between the shares of A and C is Rs. 540, then the value of x is :
x रुपये की राशि A, B और C में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 6 : 7 है तथा B और C के हिस्सों का अनुपात 3 :2 है | यदि A और C के हिस्सों में 540 रुपये का अंतर है, तो x का मान क्या होगा ?03:21View SolutionTwo numbers A and B are, respectively, 80% and 20% more than a third number C. The ratio of the numbers A to B is:
दो संख्या A और B क्रमशः, 80% और 20% अधिक है एक तीसरी संख्या C से । A से B की संख्या का अनुपात हैView Solution

