LL1 is the latus rectum of an ellipse and △S1LL1 is an equilateral triangle. Then e =Solution in Telugu
1√2
1√3
1√5
√23
The correct Answer is:B
Step by step video, text & image solution for LL^(1) is the latus rectum of an ellipse and triangleS^(1)LL^(1) is an equilateral triangle. Then e = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - PRACTICE EXERCISE65videos
ELLIPSE
- BOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - EXERCISE-I52videos
ELLIPSE
- BOOK - AAKASH SERIESCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Practice Exercise62videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH SERIESCHAPTER - EXPONENTIAL SERIES EXERCISE - EXERCISE - III8videos
EXPONENTIAL SERIES
Similar Questions
If length of the major axis is 8 and e = 1√2Axes are co-ordinate axes then equation of the ellipse is
05:20View SolutionFocus (4, 0), e =12 , directrix is x -16 = 0. Then equation of the ellipse is
02:02View SolutionThe degree and order of the differential equation [1+2(dydx)2]32=5d2ydx2 are
04:59View Solution(1+3)loge3+1+322!(loge3)2+1+333!(loge3)3+.....∞ =
05:44View SolutionIf end points of one latus rectum with the point where major axis cuts directrix makes an equilateral triangle then eccentricity of ellipse is sqrt((sqrt(5)-1)/(2))
05:44View SolutionMatch the column 1 with column ll
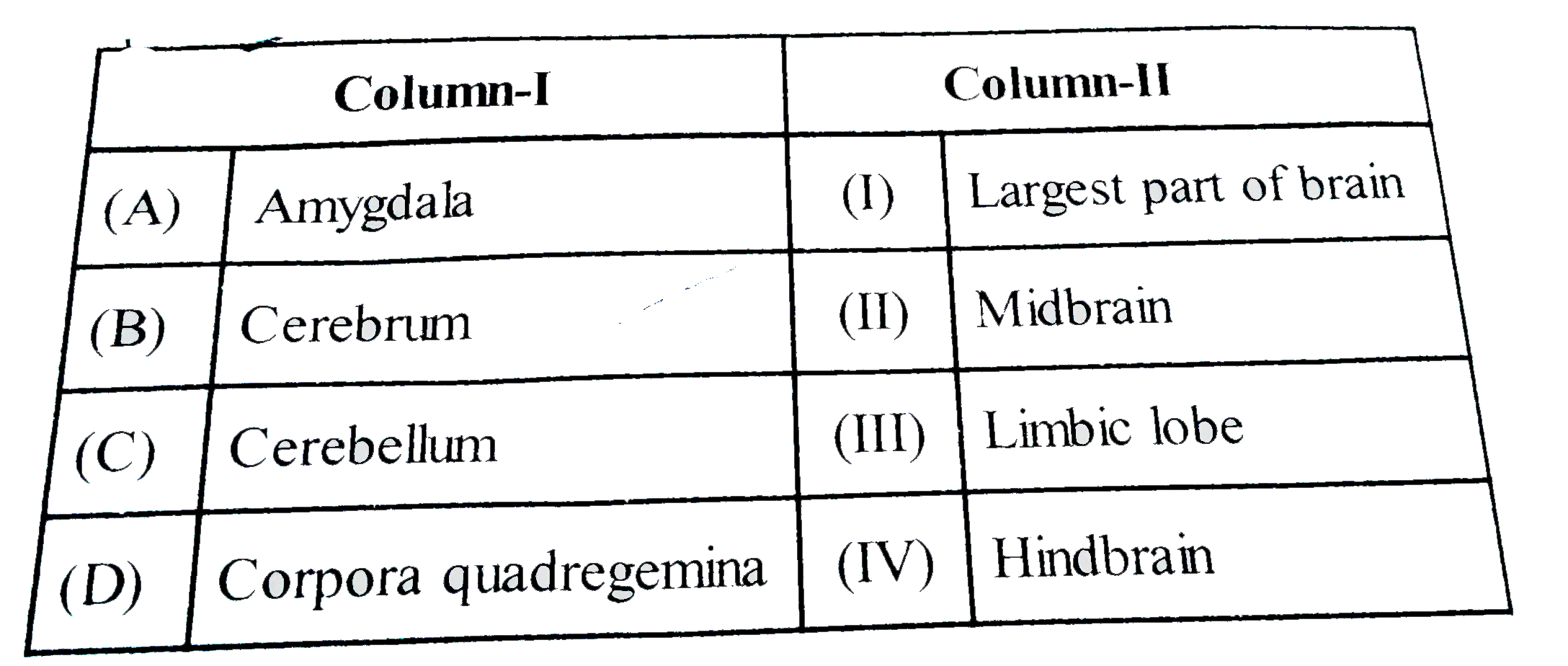 06:06View Solution
06:06View SolutionLL′ is the latusrectum of an ellipse and ΔSLL′ is an equilateral triangle. The eccentricity of the ellipse is
04:45View SolutionThe latus rectum LL′ subtends a right angle at the centre of the ellipse, then its eccentricity is
07:27View SolutionIf the latus rectum of a hyperbola forms an equilateral triangle with the vertex at the centre of the hyperbola , then its accentricity e=
02:19View SolutionLet LL' be the latus rectum through the focus S of a hyperbola and A ' be the farther vertex of the conic .If ΔA' LL' is equilateral then its eccentricity e=
05:43View SolutionThe area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
04:05View SolutionLL′ is the latus rectum of an ellipse and ΔS1LL′ is an equilateral triangle Then e=
06:12View SolutionIf C is the centre and L and L' are the ends of the latus-rectum of the ellipse x225+y216=1, then the area of the triangle CLL' is :
06:42View SolutionLL' is the latusrectum of an ellipse and ΔSLL' is an equilateral triangle.The eccentricity of the ellipse is
05:24View SolutionL=(1,3),L'=(1,−1) are the end of latus rectum of a parabola. A is the vertex of the parabola then area of ΔALL' in sq.units is
04:25View Solution

