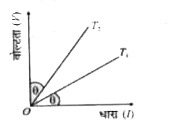
ताप T1 एवं T2पर किसी चालक के लिए V-1 ग्राफ को चित्र में दर्शाया गया है। पद (T2−T1) समानुपाती है
cos2θ
sin2θ
cot2θ
tan2θ
The correct Answer is:C
V-I वक्र का ढाल, प्रतिरोध देता है।
R1=tanθ=R0(1+αT2)
तथा R2=cotθ=R0(1+αT2)
cotθ−tanθ=R0(1+αT2)−R0(1+αT1)
=R0α(T2−T1)
या T2−T1=1αR0(cotθ−tanθ)
=1αR0(cosθsinθ−sinθcosθ)
=2cos2θαR0sin2θ=2αR0cot2θ
या T2−T1∝cot2θ
Topper's Solved these Questions
Similar Questions
एक पत्थर वेग u से क्षैतिज रूप से फेंका जाता है। 0.5 s पश्चात् पत्थर का वेग 3u/2 हो जाता है। u का मान क्या होगा ?
View Solutionबल F को इस प्रकार दिया जाता है F=at+bt2, जहाँ t समय है, तो a एवं b की विमाएँ हैं
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View Solutionp - V diagram of same mass of a gas are drawn at two different temperatures (T_1) and (T_2) . Explain whether T_1 gt T_2 or T_2 gt T_1 . .
View SolutionShow that the points (at21,2at1)(at22,2at2) and (a,0) are collinear if t1t2=−1
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig. 3.29 :-Which of the following formulae are correct for describing the motion of the particle over the time-interval t_1 to t_2 :- x(t_2)=x(t_1)+v(t_1)(t_2-t_1)+(1/2)a(t_2-t_1)^2
View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)] , [a t_2t_3,a(t_2 +t_3)] , [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionLet T bt the set of all triangle in the coordinate plane. Show that the relations in T defined as R1={(T1,T2):T1,T2∈T} T1 is similar to T2 and R2={(T1,T2):T1,T2∈T}, T1 is congruent to T2, are equivalence relations.
View SolutionWhich of the following formulae are correct for describing the motion of the particle over the time-interval t_2 to t_1 ? x(t_2)=x(t_1)+v(t_1-t_1)_+(1//2)a(t_2-t_1)^2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)] , [a t_2t_3,a(t_2 +t_3)] , [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionIf t1,t2,t3 are in A.P. (a,d) and T1,T2,T3 are in H.P. then the value of
Δ=∣∣ ∣∣t1−T1t1−T2t1−T3t2−T1t2−T2t2−T3t3−T1t3−T2t3−T3∣∣ ∣∣
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View Solution
