A marble statue of height h1 metres is mounted on a pedestal. The angles of elevation of the top and bottom of the statue from a point h2 metres above the ground level are αandβ respectively. Show that the height of the pedestal is (h1−h2)tanβ+h2tanαtanα−tanβ.
Step by step video & image solution for A marble statue of height h_1 metres is mounted on a pedestal. The angles of elevation of the top and bottom of the statue from a point h_2 metres above the ground level are alpha and beta respectively. Show that the height of the pedestal is ((h_1 - h_2)tan beta + h_2 tan alpha)/(tan alpha - tan beta). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
From the top and bottom of a building of height h metres, the angles of elevation of the top of a tower are αandβ respectively. Then the height of the tower is :
View SolutionFrom the top of a tower, the angles of depression of two objects on the same side of the tower are found to be α and β(α>β).If the distance between the objects is p metres, show that the height h of the tower is given by h=ptanαtanβtanα−tanβ metres.
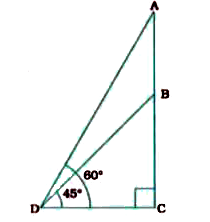
View SolutionA statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60oand from the same point the angle of elevation of the top of the pedestal is 45o. Find the height of the pedestal.
View SolutionA statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60∘ and from the samme point the angle of elevation of the top of the pedestal is 45∘. Find the height of the pedestal.
View SolutionA statue 1.6m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60∘ and from the same point the angle of elevation of the top of the pedestal is 45∘ . Find the height of the pedestal.
View SolutionIf the angle of elevation of a cloud from a point h metres above the surface of a lake is α and the angle of depression of its reflexion in the lake is β, prove that the height of the cloud is h(tanβ+tanα)tanβ−tanα metres.
View SolutionA statue, 1.6m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60∘ and from the same point the angle of elevation of the top of the pedestal is 45∘. Find the height of the pedestal.
View SolutionA bridge across a valley is h metres long. There is a temple in the valley directly below the bridge. The angles of depression of the top of the temple from the two ends of the bridge are αandβ. Prove that the height of the bridge above the top of the temple is h(tanαtanβ)tanα+tanβ metres.
View Solution
