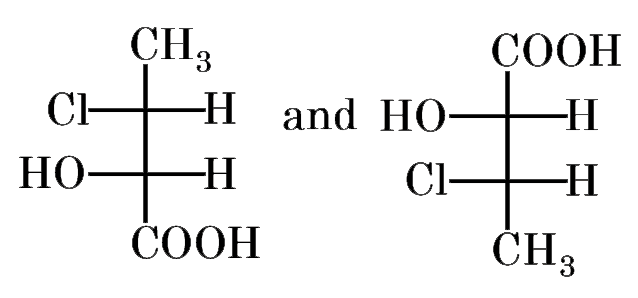Choosing a similarly related pair as the given number pair on the basis of the relation between the numbers in each pair .
12 : 169 : : ? : ?
7:50
11:144
15:240
5:49
The correct Answer is:B
To solve the analogy problem given, we need to identify the relationship between the numbers in the pair 12 and 169, and then apply that same relationship to find the corresponding pair.
1. Identify the relationship between the numbers 12 and 169.
- The number 169 can be expressed as 12+1 squared.
- Calculation: 12+1=13 and 132=169.
2. Establish the formula based on the identified relationship.
- If we denote the first number in the new pair as x, then the second number should be (x+1)2.
- This means for any number x, the second number will be the square of x+1.
3. Test possible values for x to find a suitable pair.
- Let's try x=7:
- 7+1=8 and 82=64. So the pair would be 7:64.
- Next, try x=11:
- 11+1=12 and 122=144. So the pair would be 11:144.
- Continue testing other values:
- For x=15: 15+1=16 and 162=256, giving 15:256.
- For x=5: 5+1=6 and 62=36, giving 5:36.
4. Compare the results with the options provided.
- The pairs we found are 7:64, 11:144, 15:256, and 5:36.
- Among these, the pair 11:144 matches one of the options provided.
5. Conclusion:
- The correct answer to the analogy is 11:144.
Final Answer:
The answer is 11:144.
- The number 169 can be expressed as 12+1 squared.
- Calculation: 12+1=13 and 132=169.
- If we denote the first number in the new pair as x, then the second number should be (x+1)2.
- This means for any number x, the second number will be the square of x+1.
- Let's try x=7:
- 7+1=8 and 82=64. So the pair would be 7:64.
- Next, try x=11:
- 11+1=12 and 122=144. So the pair would be 11:144.
- Continue testing other values:
- For x=15: 15+1=16 and 162=256, giving 15:256.
- For x=5: 5+1=6 and 62=36, giving 5:36.
- The pairs we found are 7:64, 11:144, 15:256, and 5:36.
- Among these, the pair 11:144 matches one of the options provided.
- The correct answer to the analogy is 11:144.
The answer is 11:144.
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - ILLUSTRATIVE EXAMPLES ( TYPE V)5videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - EXERCISE ( TYPE I)25videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - ILLUSTRATIVE EXAMPLES ON NUMBER ANALOGY4videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ALPHABET TESTEXERCISE - EXERCISE45videos
ALPHABET TEST
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALYTICAL REASONINGEXERCISE - EXERCISE24videos
ANALYTICAL REASONING
Similar Questions
Knowledge Check
- Question 1 - Select One
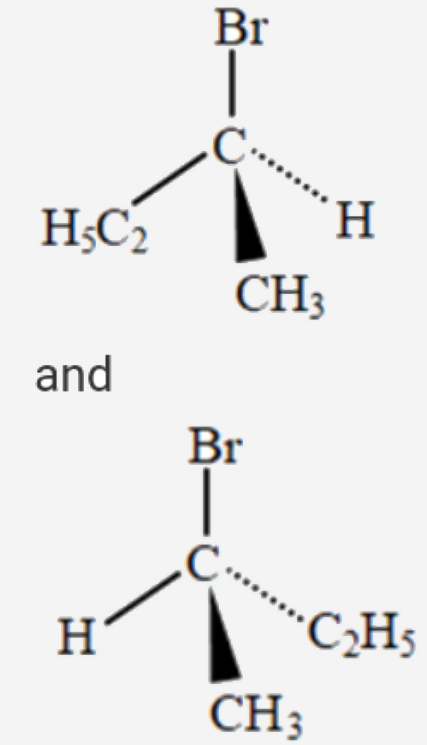
Relation between given pair is :AenantiomerBdoasterep,erCodemtoca,Dstrictural isomer - Question 2 - Select One
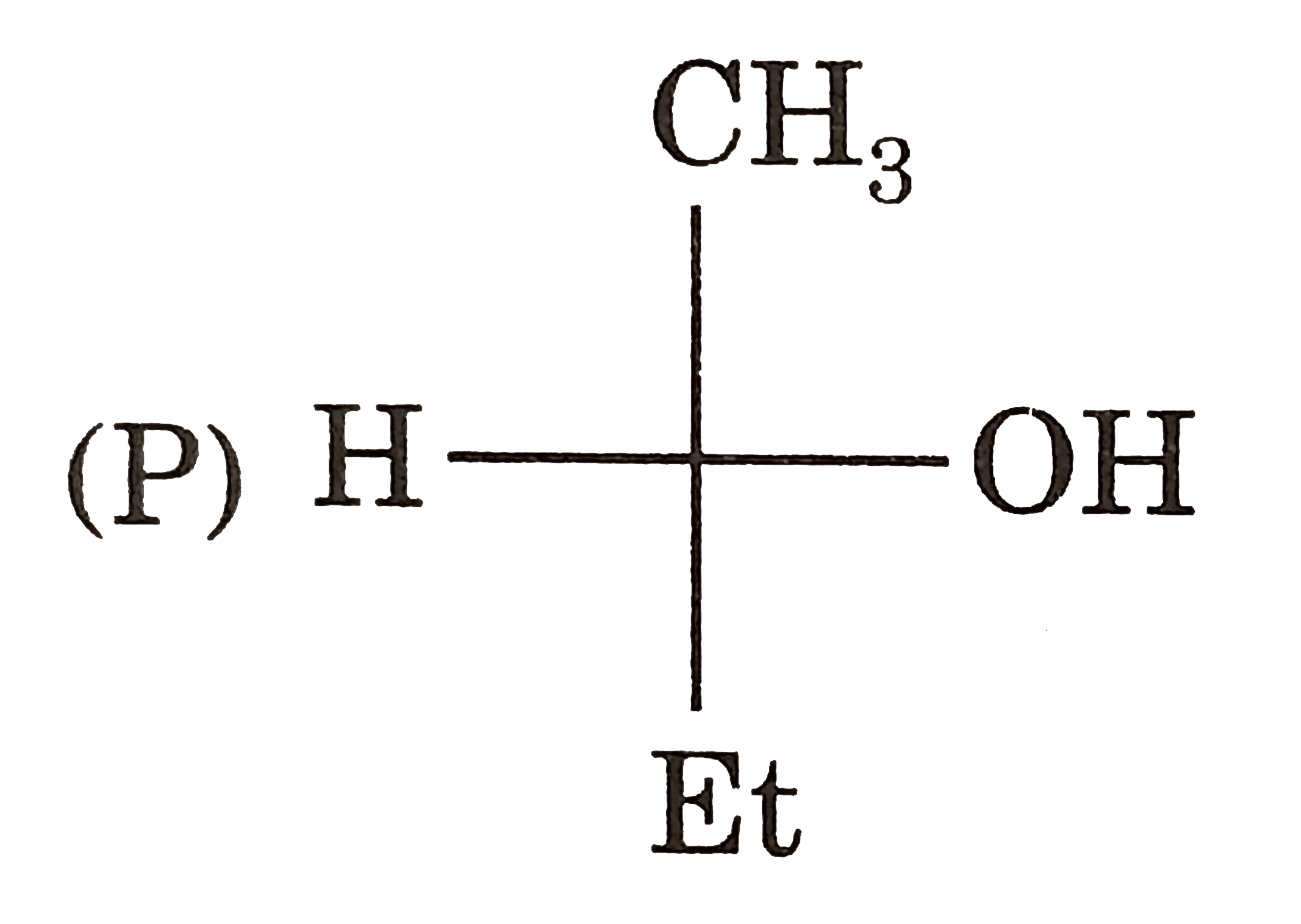
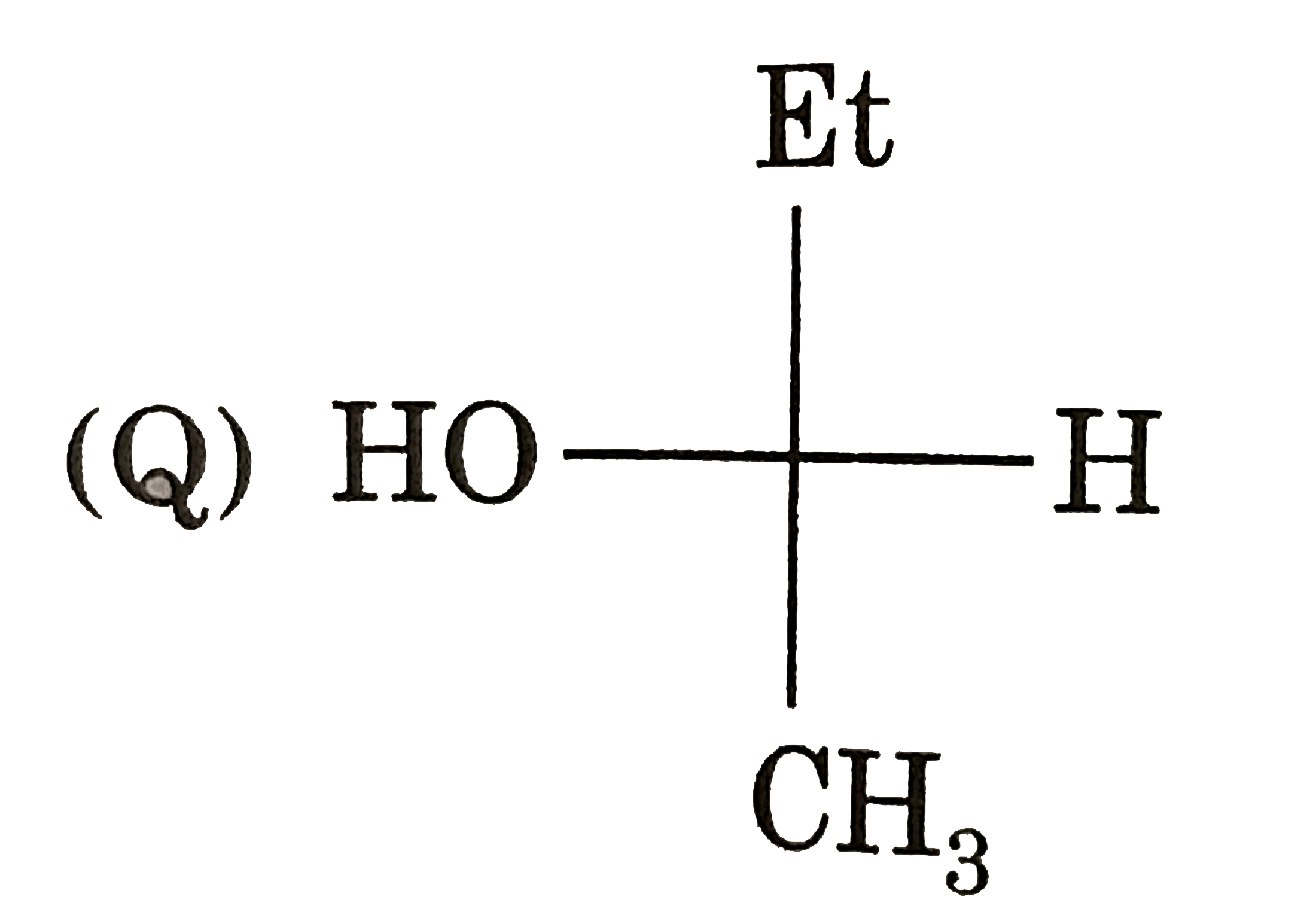
Relation between gives pair is -
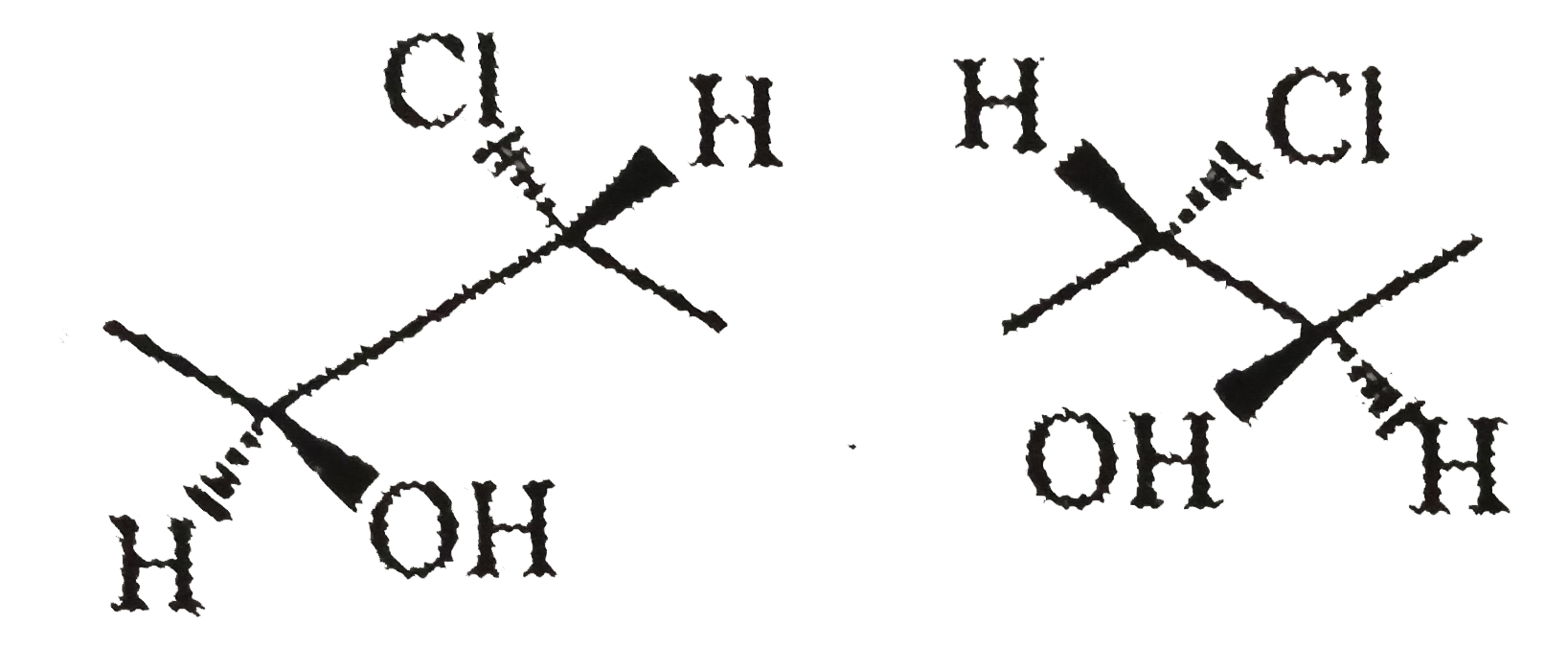 AEnantiomerBDiastereomersCIdenticalDStructural isomer
AEnantiomerBDiastereomersCIdenticalDStructural isomer - Question 3 - Select One
What is relation between the following pairs
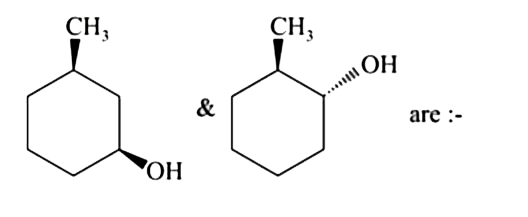 AidenticalBGeometrical isomerCPositional isomerD(2) & (3) both
AidenticalBGeometrical isomerCPositional isomerD(2) & (3) both
Choosing a number related to a given number in the same manner as the two numbers of another given pair are related to each other
4 : 19 ::7 : ?View SolutionChoosing a number related to a given number in the same manner as the two numbers of another given pair are related to each other
82 : 9 :: 26 : ?View SolutionChoosing a number related to a given number in the same manner as the two numbers of another given pair are related to each other
8 : 32 :: 10: ?View SolutionWhich of the following is incorrect relation between given pairs ?
View SolutionChoosing a number related to a given number in the same manner as the two numbers of another given pair are related to each other
48 : 122 :: 168 : ?View Solution