Circle : Diameter ::?:?
Rectangle : Diagonal
Diameter: Radius
Square : Rectangle
Bisector : Angle
The correct Answer is:A
To solve the analogy "Circle : Diameter :: ? : ?", we need to identify the relationship between the first pair of words (Circle and Diameter) and find a similar relationship in the second pair.
1. Identify the Relationship:
- A circle is a geometric shape, and the diameter is a line segment that passes through the center of the circle and touches two points on its boundary. The diameter divides the circle into two equal halves.
2. Find a Similar Pair:
- We need to find a pair of words where the second word divides the first word into two equal parts, just like the diameter divides the circle.
3. Evaluate the Options:
- Option 1: Rectangle, Diagonal:
- A diagonal of a rectangle divides it into two equal triangles. This fits the relationship.
- Option 2: Diameter, Radius:
- The radius does not divide the diameter into two equal parts; it is a different relationship.
- Option 3: Square, Rectangle:
- A square is a specific type of rectangle, but it does not divide it into equal parts.
- Option 4: Bisector, Angle:
- A bisector divides an angle into two equal parts, but the relationship is reversed in the analogy.
4. Choose the Correct Option:
- Since the diagonal of a rectangle divides it into two equal parts, the correct answer is Option 1: Rectangle, Diagonal.
Final Answer:
Rectangle : Diagonal
- A circle is a geometric shape, and the diameter is a line segment that passes through the center of the circle and touches two points on its boundary. The diameter divides the circle into two equal halves.
- We need to find a pair of words where the second word divides the first word into two equal parts, just like the diameter divides the circle.
- Option 1: Rectangle, Diagonal:
- A diagonal of a rectangle divides it into two equal triangles. This fits the relationship.
- Option 2: Diameter, Radius:
- The radius does not divide the diameter into two equal parts; it is a different relationship.
- Option 3: Square, Rectangle:
- A square is a specific type of rectangle, but it does not divide it into equal parts.
- Option 4: Bisector, Angle:
- A bisector divides an angle into two equal parts, but the relationship is reversed in the analogy.
- Since the diagonal of a rectangle divides it into two equal parts, the correct answer is Option 1: Rectangle, Diagonal.
Rectangle : Diagonal
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - EXERCISE ( TYPE IV)30videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - EXERCISE ( TYPE V)15videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALOGYEXERCISE - EXERCISE ( TYPE II)20videos
ANALOGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ALPHABET TESTEXERCISE - EXERCISE45videos
ALPHABET TEST
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ANALYTICAL REASONINGEXERCISE - EXERCISE24videos
ANALYTICAL REASONING
Similar Questions
Knowledge Check
- Question 1 - Select One
The equation of the circle whose diameter is common chord to the circles
Ax2+y2−2ab2a2+b2x+2a2ba2+b2y+c=0Bx2+y2−2ab2a2+b2x+2a2ba2+b2y+c=0Cx2+y2+2ab2a2+b2x+2a2ba2+b2y+c=0Dx2+y2+2ab2a2+b2x−2a2ba2+b2y+c=0
Find the circumference and area of a circle of diameter 49 m
View SolutionFind the area of a circle of diameter 7 cm.
View SolutionFind the circumference and area of a circle of diameter 28cm
View SolutionCircumference of a circle of diameter 5 cm is
View SolutionFind the circumference and area of a circle of diameter of 28 cm.
View SolutionIn the given circle with diameter AB find the value of x.
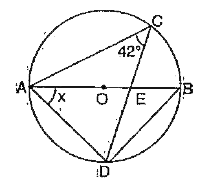 View Solution
View SolutionFind the area of circle whose diameter is 21 cm
View Solution

