−−G−C−GK−PG−
KCPCPK
CPKPCK
PKCPKP
CPPKCP
The correct Answer is:B
To solve the series −−G−C−GK−PG−, we need to identify the pattern in the sequence and fill in the blanks accordingly.
1. Identify the given elements: The series has some letters filled in and some blanks. The letters present are G, C, GK, and PG.
2. Group the elements: We can divide the series into groups of letters. The series can be observed in segments:
- First segment: −−G−
- Second segment: C−GK−
- Third segment: PG−
3. Analyze the segments:
- In the first segment, we have two blanks before G and one blank after G.
- In the second segment, we have C followed by a blank and then GK.
- In the third segment, we have PG followed by a blank.
4. Look for a pattern:
- If we observe the letters, we can try to create a sequence.
- The letters G, C, GK, and PG can be arranged or repeated in a certain order.
5. Establish a sequence:
- Let's assume a repeating pattern of letters.
- We can try to fill in the blanks with letters that would create a consistent pattern.
- Based on the letters we have, we can try to fill in the blanks with C, P, G, and K in a repeating manner.
6. Fill in the blanks:
- If we fill the first blank with C, the second blank with P, the third blank with K, the fourth blank with C, and the fifth blank with K, we can create a pattern.
- Thus, we can fill the series as:
- C P G C K G K P G
7. Check for consistency:
- After filling in the blanks, we can check if the pattern holds.
- The sequence maintains a consistent order and repeats the letters in a logical manner.
8. Select the correct option:
- Based on the filled sequence, we can compare it with the given options.
- The option that matches our filled sequence is option B.
Final Answer:
The answer is option B.
- First segment: −−G−
- Second segment: C−GK−
- Third segment: PG−
- In the first segment, we have two blanks before G and one blank after G.
- In the second segment, we have C followed by a blank and then GK.
- In the third segment, we have PG followed by a blank.
- If we observe the letters, we can try to create a sequence.
- The letters G, C, GK, and PG can be arranged or repeated in a certain order.
- Let's assume a repeating pattern of letters.
- We can try to fill in the blanks with letters that would create a consistent pattern.
- Based on the letters we have, we can try to fill in the blanks with C, P, G, and K in a repeating manner.
- If we fill the first blank with C, the second blank with P, the third blank with K, the fourth blank with C, and the fifth blank with K, we can create a pattern.
- Thus, we can fill the series as:
- C P G C K G K P G
- After filling in the blanks, we can check if the pattern holds.
- The sequence maintains a consistent order and repeats the letters in a logical manner.
- Based on the filled sequence, we can compare it with the given options.
- The option that matches our filled sequence is option B.
The answer is option B.
Topper's Solved these Questions
- SERIES COMPLETION TEST BOOK - MCGROW HILL PUBLICATIONCHAPTER - SERIES COMPLETION TEST EXERCISE - EXERCISE 3 TYPE III
10 Videos
- SERIES BOOK - MCGROW HILL PUBLICATIONCHAPTER - SERIES EXERCISE - ILLUSTRATIVE EXAMPLES
3 Videos
- SITUATION REACTION TEST BOOK - MCGROW HILL PUBLICATIONCHAPTER - SITUATION REACTION TEST EXERCISE - EXERCISE
15 Videos
Similar Questions
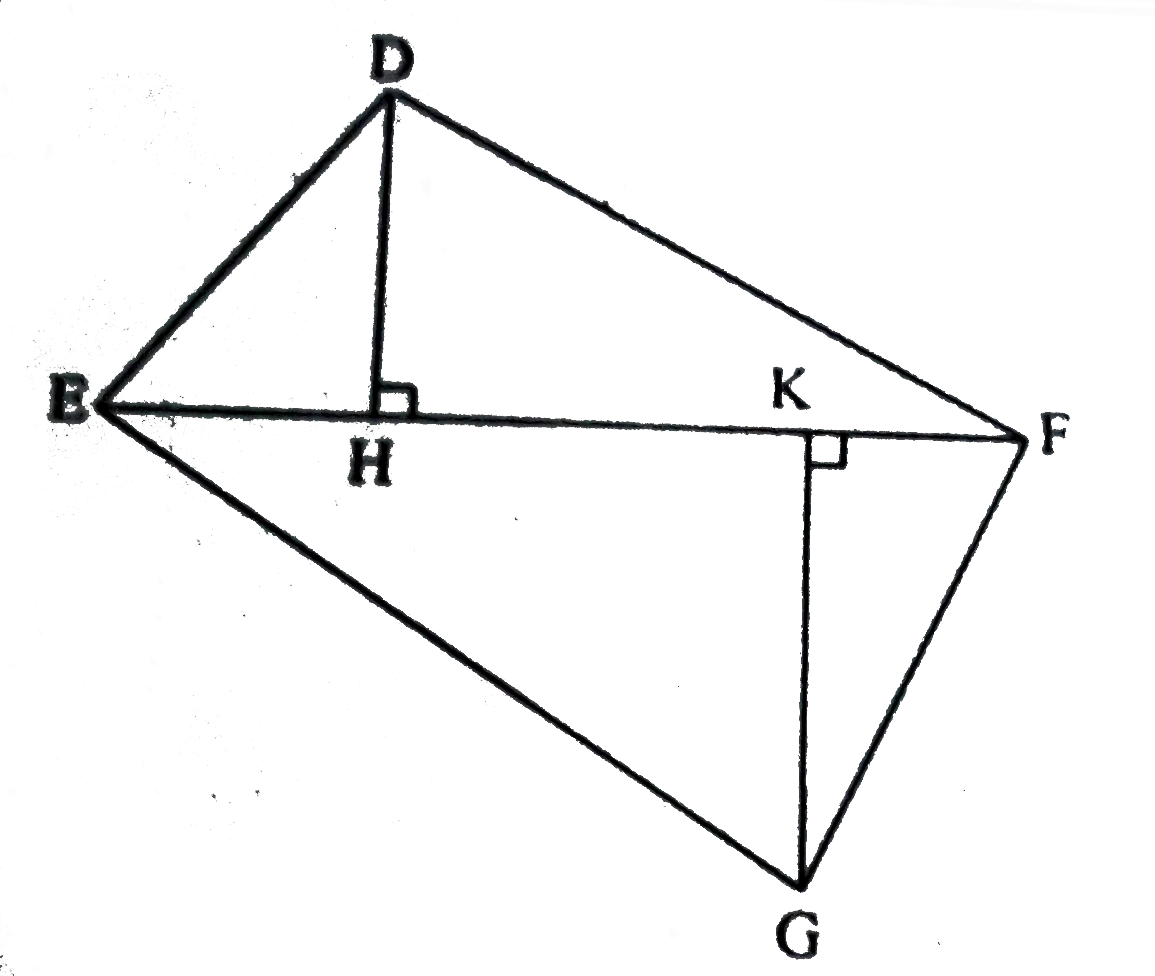
In the following figure, seg DH⊥seg EF and seg GK⊥EF. If DH = 6 cm, GK = 10 cm and A(ΔDEF) = 150cm2, then find:
(i) EF
(ii) A(ΔGEF)
(iii) A(□DFGE)
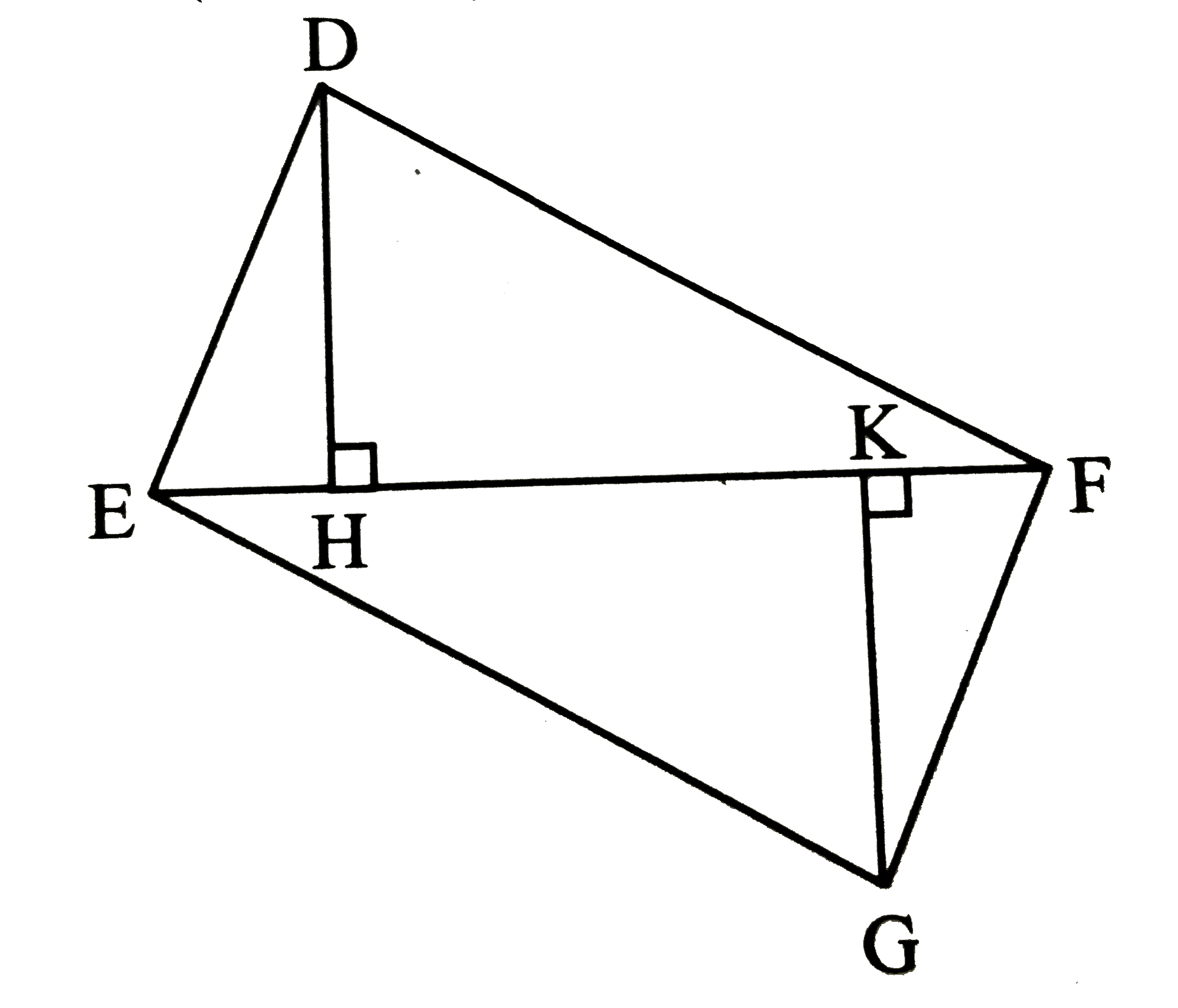
View SolutionIn the following figure,segDH⊥segEFandsegGK⊥segEF.IfDH=6cm,GK=10cmandA(ΔDEF)=150cm2, then find :
i.EF
ii.A(ΔGEF)
iii.A(□DFGE).
View Solution
Knowledge Check
If PA is the median of the triangle PQR and G be the centroid, then what is the ratio of (PA+GA):(PG−GA)?
A4:1B3:1C2:1D3:2If PA is the median of the triangle PQR and G be the centroid, then what is the ratio of (PA+GA):(PG−GA)?
A4:1B3:1C2:1D3:2Find the missing (?) in the series
AB, CE, FI , ?, OT
A. JM
B. GK
C. HO
D. JNADBACCDB
If in rectangular hyperbola normal at any point P meet the axes in G and g and C be centre of hyperbola then (A) PG=Pg (B)PG=PC (C)Pg=PC (D)None
View SolutionIf the normal at P to the rectangular hyperbola x2−y2=4 meets the axes at G and gandC is the center of the hyperbola, then PG=PC (b) Pg=PC PG−Pg (d) Gg=2PC
View SolutionSelect the option that represents the letters that, when placed from left to right in the blanks below, will complete the letter series. G _ R_ M_ KRC_ GK_ CM
View SolutionIf the normal at any point on the ellipse x2a2+y2b2=1. Meet the major & minor axes at G and g such that PG:Pg=1:5 and area of ΔCBS=10 sq. units C is centre of ellipse S is focus & B in one end of minor axis, then
View SolutionIf PG1 and PG2 be the normals to the curves y2=4ax and ay2=4x3 at a common point other than origin meeting x-axis in G1 and G2 , then G1G2 =
View Solution
