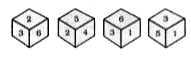
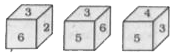
Six dice with their top faces raised as shown below. The sum of the number of dots on the opposite faces is 7.

If the dice (i), (ii), (iii) have even number of dots on their bottom faces, then what would be the total number of dots on the top faces?
A
14
B
7
C
21
D
12
Text Solution
The correct Answer is:B
Since total on opposite faces is 7 so opposite faces contain (1, 6), (2, 5), (3, 4).
∴ hidden faces in all the six dice are as follow,
Fig. (i) : 3↔4 Fig. (ii) : 1↔6 Fig. (iii) : 3↔4
Fig. (iv) : 1↔6 Fig. (v) : 3↔4 Fig. (vi) : 1↔6
In Figs (i), (ii) and (iii), even dots are at bottom faces, so in the top faces, the numbers are 3, 1 and 3.
∴ Sum is 3 + 1 + 3 i.e. 7.
|
Topper's Solved these Questions
- PROBLEMS ON CUBES AND DICEBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBLEMS ON CUBES AND DICEEXERCISE - EXERCISE 3
20 Videos
- PROBLEMS ON CLOCKSBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBLEMS ON CLOCKSEXERCISE - EXERCISE
20 Videos
- PUZZLE TESTBOOK - MCGROW HILL PUBLICATIONCHAPTER - PUZZLE TESTEXERCISE - Exercise
25 Videos
Similar Questions
Knowledge Check
Based in the given position of the dice find the number of dots on the face opposite to the face with one dot.
 A2B3C4D6
A2B3C4D6Two positions of a DICE are shown. What number must on the opposite face of 4?
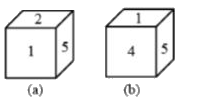 A5B4C3D2
A5B4C3D2Three positions of a dice are given below
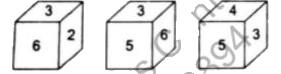
Identity the number on the face opposite to 6.A1B4C5D7
Four portions of a dice are shown below: Which number is on the face opposite to 3?
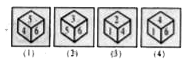
View SolutionThree positions of a dice are given below. Identify the number on the face opposite to 6.
View SolutionTwo different positions of a dice are give below. What will be the number of dots on the face opposite the face having 2 dots.
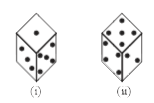
View SolutionTwo different positions of a dice are give below. What will be the number of dots on the face opposite the face having 2 dots.

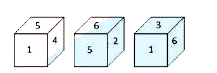
View SolutionThree different positions of a dice are shown below. Which number appears on the face opposite number 3 ?
View Solution