Sphere : Ball :: ?
Circle : Disc
Cube : Dice
Line : rope
Triangle : cone
The correct Answer is:B
To solve the analogy question "Sphere : Ball :: ?," we need to identify the relationship between the first pair and apply it to find the second pair.
1. Identify the Relationship in the First Pair:
- The first term is "Sphere," which is a three-dimensional geometric shape.
- The second term is "Ball," which is a common object that takes the shape of a sphere.
2. Determine the Characteristics:
- Both "Sphere" and "Ball" represent the same three-dimensional shape. A ball is essentially a physical representation of a sphere.
3. Look for a Similar Relationship in the Options:
- We need to find a pair where the first term is a three-dimensional shape, and the second term is a common object that represents that shape.
4. Evaluate the Options:
- Let’s consider the options:
- A. Disc : Circle (Both are 2D shapes)
- B. Cube : Dice (Both are 3D shapes)
- C. Line : Point (1D and 0D shapes)
- D. Triangle : Pyramid (2D and 3D shapes)
- The only option that maintains the same 3D relationship as "Sphere : Ball" is "Cube : Dice."
5. Conclusion:
- Therefore, the answer to the analogy is "Cube : Dice."
Final Answer:
Sphere : Ball :: Cube : Dice
- The first term is "Sphere," which is a three-dimensional geometric shape.
- The second term is "Ball," which is a common object that takes the shape of a sphere.
- Both "Sphere" and "Ball" represent the same three-dimensional shape. A ball is essentially a physical representation of a sphere.
- We need to find a pair where the first term is a three-dimensional shape, and the second term is a common object that represents that shape.
- Let’s consider the options:
- A. Disc : Circle (Both are 2D shapes)
- B. Cube : Dice (Both are 3D shapes)
- C. Line : Point (1D and 0D shapes)
- D. Triangle : Pyramid (2D and 3D shapes)
- The only option that maintains the same 3D relationship as "Sphere : Ball" is "Cube : Dice."
- Therefore, the answer to the analogy is "Cube : Dice."
Sphere : Ball :: Cube : Dice
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-3(ANALOGY)EXERCISE - TYPE 3 [Number Analogy]30videos
ASSIGNMENT-3(ANALOGY)
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-3(ANALOGY)EXERCISE - TYPE 425videos
ASSIGNMENT-3(ANALOGY)
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-3(ANALOGY)EXERCISE - TYPE 5 [Double Analogy]20videos
ASSIGNMENT-3(ANALOGY)
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-10 (CLASSIFICATION)EXERCISE - TYPE-420videos
ASSIGNMENT-10 (CLASSIFICATION)
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-7 (PUZZLE TEST)EXERCISE - MCQs20videos
ASSIGNMENT-7 (PUZZLE TEST)
Similar Questions
You move a ball of mass m away form a sphere of mass M. (a) Does the gravitational patential energy of the systemof ball and sphere increase or decrease ? (b) Is positive work or negative work done by the gravitational force between the ball and the sphere ?
View SolutionA solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle θ to the horizontal. Find the acceleration of the ball.
View Solution
Knowledge Check
- Question 1 - Select One
A small spherical ball of mass m is projected from lowest point (point P) in the space between two fixed, concentric spheres A and B (see figure). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. Speed of ball at lowest point is v. NA and NB represent magnitudes of the normal reaction force on the ball exerted by the spheres A and B respectively. Match the value of v given in column–I with corresponding results in column–II.
 AColumn-IColumn-II(A)v=√gR(p)maximum value of NA=0BColumn-IColumn-II(B)v=√2gR(q)minimum value of NB=0CColumn-IColumn-II(C)v=√3gR(r)maximum value of NB=6mgDColumn-IColumn-II(D)v=√5gR(s)maximum value of NB=4mg(t)maximum value of NB=2mg
AColumn-IColumn-II(A)v=√gR(p)maximum value of NA=0BColumn-IColumn-II(B)v=√2gR(q)minimum value of NB=0CColumn-IColumn-II(C)v=√3gR(r)maximum value of NB=6mgDColumn-IColumn-II(D)v=√5gR(s)maximum value of NB=4mg(t)maximum value of NB=2mg - Question 2 - Select One
A lead sphere is dropped into a medium. As the sphere falls, the velocity of lead sphere
Aremains constant throughoutBdecreases and finally becomes zeroCdecreases for some time and then becomes constantDincreases for some time and then decreases - Question 3 - Select One
Assertion : A cricket ball has a shape of a sphere.
Reason : A ball-like shape is called a sphere.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA spherical ball of lead of radius 14 cm is melted and recast into spheres of radius 2 cm. The number of the small spheres is
View SolutionA solid spherical ball of iron of radius 4 cm is melted to form spheres of radius 2 cm each The number of spheres so formed is
View SolutionA spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas.View SolutionTwo uncharged conducting spheres, A and B, are suspended from insulating threads so that they touch each other as shown in the figure. While a negatively charged rod is held near, but not touching sphere A, someone moves ball B away from A. How will the spheres be charged, if at all ?
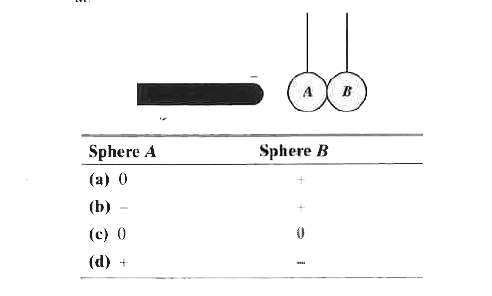 View Solution
View Solution

