Let A = (abcd) be such that A3=O but A≠O then
A2=O
A2=A
A2=I−A
none of these
The correct Answer is:A
To solve the problem, we need to analyze the properties of the matrix A given that A3=O (the null matrix) and A≠O.
1. Given Information: We know that A3=O and A≠O.
2. Post-Multiplying by A−1: Since A is not the null matrix, we can consider the possibility of finding A−1 (the inverse of A). However, we need to be careful because A being nilpotent (since A3=O) implies that it cannot have an inverse. Thus, we cannot directly multiply by A−1.
3. Analyzing A3=O: Since A3=O, we can express this as:
A⋅A⋅A=O
This indicates that multiplying A by itself three times results in the null matrix.
4. Exploring the Implications: From the property of nilpotent matrices, we can conclude that:
- A2 cannot be the identity matrix I because if A2=I, then A3 would not be O.
- Therefore, A2 must also be a nilpotent matrix.
5. Finding A2: Since A3=O implies that A2 must also be such that:
A2⋅A=O
This means A2 must also be a non-invertible matrix (since it leads to the null matrix when multiplied by A).
6. Conclusion: The only conclusion we can draw is that:
A2=O
This is consistent with the properties of nilpotent matrices.
Final Result:
Thus, we conclude that A2=O.
A⋅A⋅A=O
This indicates that multiplying A by itself three times results in the null matrix.
- A2 cannot be the identity matrix I because if A2=I, then A3 would not be O.
- Therefore, A2 must also be a nilpotent matrix.
A2⋅A=O
This means A2 must also be a non-invertible matrix (since it leads to the null matrix when multiplied by A).
A2=O
This is consistent with the properties of nilpotent matrices.
Thus, we conclude that A2=O.
Topper's Solved these Questions
- MATRICESBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATRICESEXERCISE - SOLVED EXAMPLES ( LEVEL 2 ( Straight Objective Type Questions ) )
11 Videos
- MATRICESBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATRICESEXERCISE - SOLVED EXAMPLES ( LEVEL 2 (Numercial Answer Type Questions))
18 Videos
- MATRICESBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATRICESEXERCISE - Questions from Previous Years. B -Architecture Entrance Examination Papers
22 Videos
- MATHEMATICAL REASONING BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL REASONING EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B. ARCHITECTURE ENTRANCE EXAMINATION PAPERS
11 Videos
- PARABOLABOOK - MCGROW HILL PUBLICATIONCHAPTER - PARABOLAEXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTRE ENTRANCE EXAMINATION PAPERS
9 Videos
Similar Questions
Knowledge Check
If A = [abcd] such that A satisfies the relation A2−(a+d)A=O then inverse of A is
AIBAC(a+d)ADnone of these
If A=[abcd], where a, b, c and d are real numbers, then prove that A2−(a+d)A+(ad−bc)I=O. Hence or therwise, prove that if A3=O then A2=O
View SolutionABCD is a trapezium such that BC∣∣AD and AB=4cm . If the diagonals AC and BD intersect at O such that AOOC=DOOB=12 , then BC= 7cm (b) 8cm (c) 9cm (d) 6cm
View SolutionA point O is taken inside an equilateral four sided figure ABCD such that its distances from the angular points D and B are equal. Show that AO and OC are in one and the same straight line. GIVEN : A point O inside an equilateral quadrilateral four sided figure ABCD such that BO=OD. TO PROVE : AO and OC are in one and the same straight line.
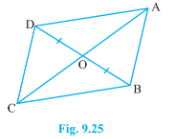
View SolutionIn Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= 1000 (b) 800 (c) 900 (d) 1350
View SolutionIf ABC and DEF are similar triangles such that ∠A=47o and ∠E=83o , then ∠C= 50o (b) 60o (c) 70o (d) 80o
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View Solution
