Consider the lines
L1:x+y=10, L2:x+y=60
L3:x=40, L4:y=40.
L1 meets x - axis and y - axis at A and B respectively.
L4 meets y - axis at C and L2 at D
L3 meets L2 at E and x-axis at F.
Perimeter of the hexagon ABCDEF is
100+50√2
50+40√2
100
none of these
The correct Answer is:A
To find the perimeter of the hexagon ABCDEF formed by the intersection of the given lines, we will follow these steps:
Step 1: Find the coordinates of point A
The line L1:x+y=10 meets the x-axis when y=0.
Substituting y=0 into the equation:
x+0=10⟹x=10
Thus, the coordinates of point A are A(10,0).
Step 2: Find the coordinates of point B
The line L1:x+y=10 meets the y-axis when x=0.
Substituting x=0 into the equation:
0+y=10⟹y=10
Thus, the coordinates of point B are B(0,10).
Step 3: Find the coordinates of point C
The line L4:y=40 meets the y-axis when x=0.
Thus, the coordinates of point C are C(0,40).
Step 4: Find the coordinates of point D
The line L2:x+y=60 meets the y-axis when x=0.
Substituting x=0 into the equation:
0+y=60⟹y=60
Thus, the coordinates of point D are D(0,60).
Step 5: Find the coordinates of point E
The line L3:x=40 intersects line L2:x+y=60.
Substituting x=40 into the equation:
40+y=60⟹y=20
Thus, the coordinates of point E are E(40,20).
Step 6: Find the coordinates of point F
The line L3:x=40 meets the x-axis when y=0.
Thus, the coordinates of point F are F(40,0).
Step 7: Calculate the lengths of the sides of the hexagon
1. Length AB:
AB=√(10−0)2+(0−10)2=√102+(−10)2=√100+100=10√2
2. Length BC:
BC=√(0−0)2+(10−40)2=√0+(−30)2=30
3. Length CD:
CD=√(0−0)2+(40−60)2=√0+(−20)2=20
4. Length DE:
DE=√(0−40)2+(60−20)2=√(−40)2+(40)2=√1600+1600=40√2
5. Length EF:
EF=√(40−40)2+(20−0)2=√0+202=20
6. Length FA:
FA=√(40−10)2+(0−0)2=√(30)2+0=30
Step 8: Calculate the perimeter of hexagon ABCDEF
The perimeter P is the sum of all the lengths:
P=AB+BC+CD+DE+EF+FA
Substituting the lengths we found:
P=10√2+30+20+40√2+20+30
Combining like terms:
P=(10√2+40√2)+(30+20+20+30)=50√2+100
Final Answer
The perimeter of the hexagon ABCDEF is:
P=50√2+100
The line L1:x+y=10 meets the x-axis when y=0.
Substituting y=0 into the equation:
x+0=10⟹x=10
Thus, the coordinates of point A are A(10,0).
The line L1:x+y=10 meets the y-axis when x=0.
Substituting x=0 into the equation:
0+y=10⟹y=10
Thus, the coordinates of point B are B(0,10).
The line L4:y=40 meets the y-axis when x=0.
Thus, the coordinates of point C are C(0,40).
The line L2:x+y=60 meets the y-axis when x=0.
Substituting x=0 into the equation:
0+y=60⟹y=60
Thus, the coordinates of point D are D(0,60).
The line L3:x=40 intersects line L2:x+y=60.
Substituting x=40 into the equation:
40+y=60⟹y=20
Thus, the coordinates of point E are E(40,20).
The line L3:x=40 meets the x-axis when y=0.
Thus, the coordinates of point F are F(40,0).
1. Length AB:
AB=√(10−0)2+(0−10)2=√102+(−10)2=√100+100=10√2
BC=√(0−0)2+(10−40)2=√0+(−30)2=30
CD=√(0−0)2+(40−60)2=√0+(−20)2=20
DE=√(0−40)2+(60−20)2=√(−40)2+(40)2=√1600+1600=40√2
EF=√(40−40)2+(20−0)2=√0+202=20
FA=√(40−10)2+(0−0)2=√(30)2+0=30
The perimeter P is the sum of all the lengths:
P=AB+BC+CD+DE+EF+FA
Substituting the lengths we found:
P=10√2+30+20+40√2+20+30
Combining like terms:
P=(10√2+40√2)+(30+20+20+30)=50√2+100
The perimeter of the hexagon ABCDEF is:
P=50√2+100
Topper's Solved these Questions
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS
30 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (NUMERICAL ANSWER TYPE QUESTIONS)
25 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS
15 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
17 Videos
Similar Questions
Knowledge Check
The three lines l1=4x−3y+2=0,l2=3x+4y−4=0 and l3=x−7y+6=0
Aform a rt. angled isosceles triangleBform a rt. Angled triangleCare concurrentDNoneConsider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
AThe line x+y=0 bisects the acute angle between L1and L2 containing the origin.BThe line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.CThe line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.DThe line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.A variable line L is drawn through O(0,0) to meet the line L1 and L2 given by y-x-10 =0 and y-x-20=0 at Points A and B, respectively.
Locus of P, if OP2=OA×OB, isA(y−x)2=100B(y+x)2=50C(y−x)2=200Dnone of these
Consider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
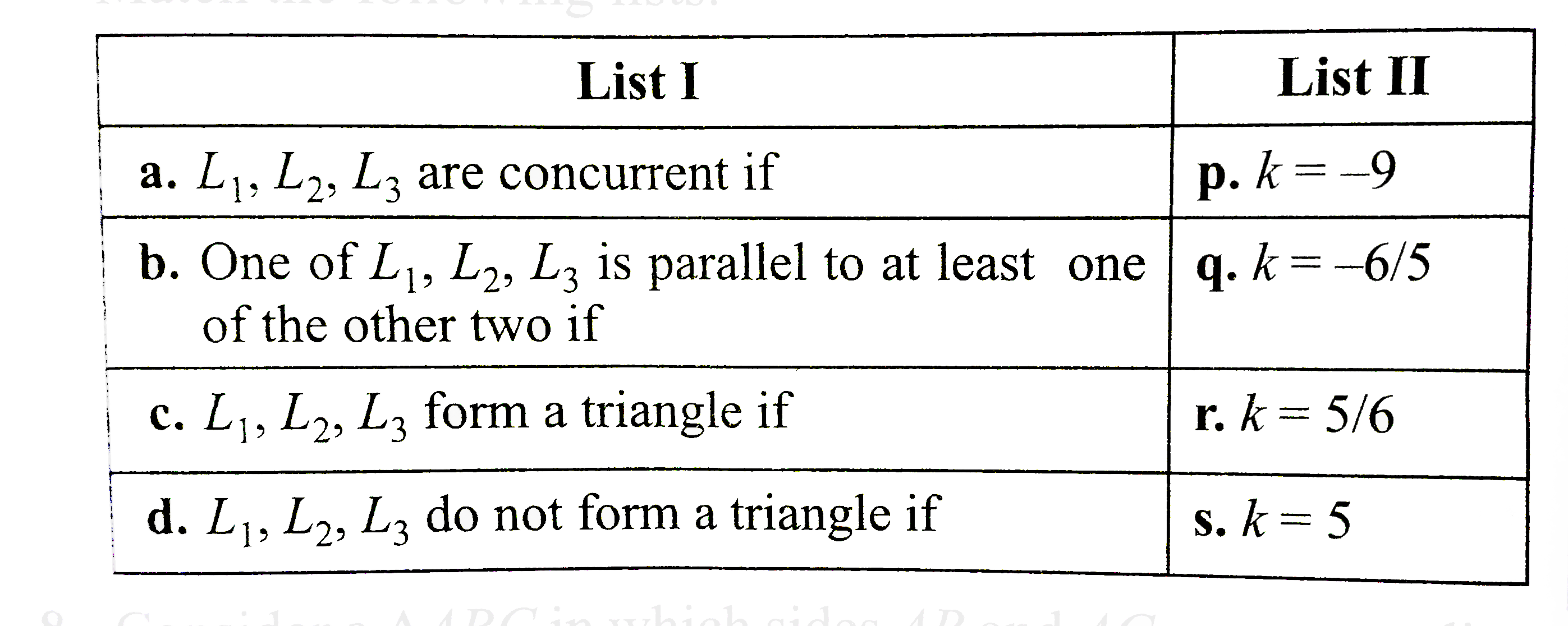
View SolutionFor the lines L1:3x−2y+5=0andL2:kx+by–15=0 L1 is perpendicular to L2 if k=4.
View SolutionLet a line L1:3x+2y−6=0 intersect the x and y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the x and y axes at R and S respectively.The locus of point of intersection of the lines PS and QR is
View SolutionThe line l in Fig14.14 meets X-axis at A(-5,0) and Y-axis at B(0,-3).
View SolutionConsider the following lines :
L1:x−y−1=0
L2:x+y−5=0
L3:y−4=0
Let L1 is axis to a parabola, L2 is tangent at the vertex to this parabola and L3 is another tangent to this parabola at some point P.
Let 'C' be the circle circumscribing the triangle formed by tangent and normal at point P and axis of parabola. The tangent and normals at normals at the extremities of latus rectum of this parabola forms a quadrilateral ABCD.
Q. The equation of the circle 'C' is :
View Solution

